
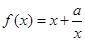 有如下性質:如果常數
有如下性質:如果常數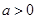 ,那么該函數在
,那么該函數在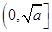 上是減函數,在
上是減函數,在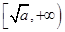 上是增函數.
上是增函數.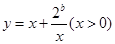 在
在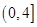 上是減函數,在
上是減函數,在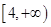 上是增函數,求
上是增函數,求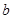 的值;
的值;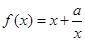 (常數
(常數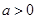 )在
)在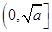 上是減函數;
上是減函數;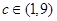 ,求函數
,求函數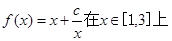 的最小值和最大值.
的最小值和最大值.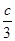 ;
;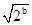 =4,由此可知b=4.
=4,由此可知b=4.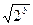 ="4," ∴b=4.
="4," ∴b=4.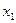 ,
,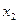 ∈
∈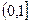 ,且
,且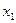 <
<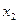 , ∵
, ∵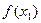 -
-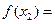
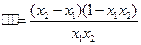 ,
,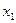 ,
,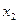 ∈
∈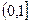 ,
,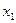 <
<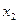 得0<
得0<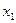
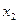 <1,1-
<1,1-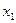
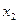 >0,故
>0,故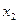 -
-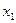 >0 ,于是
>0 ,于是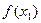 -
-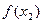 >0,
>0,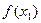 >
> 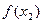 .∴
.∴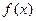 =
= 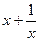 在
在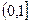 上是減函數.
上是減函數.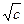 ∈[1,3], 于是,當x=
∈[1,3], 于是,當x=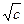 時, 函數f(x)=x+
時, 函數f(x)=x+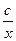 取得最小值2
取得最小值2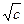 .
. ,所以:
,所以: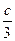 ;
;

科目:高中數學 來源:不詳 題型:解答題
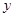 (萬元)與處理量
(萬元)與處理量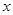 (噸)之間的函數關系可近似地表示為:
(噸)之間的函數關系可近似地表示為: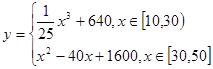 , 且每處理一噸二氧化碳可得價值為
, 且每處理一噸二氧化碳可得價值為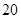 萬元的某種化工產品.
萬元的某種化工產品. 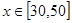 時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損?
時,判斷該技術改進能否獲利?如果能獲利,求出最大利潤;如果不能獲利,則國家至少需要補貼多少萬元,該工廠才不虧損? 查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.f (x)=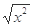 , g(x)=x , g(x)=x | B.f (x)=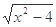 , g(x)= , g(x)=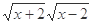 |
C.f (x)=x, g(x)=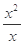 | D.f (x)=|x+1|, g(x)=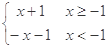 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
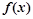 的定義域為D,若存在非零常數l使得對于任意
的定義域為D,若存在非零常數l使得對于任意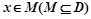 有
有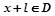 且
且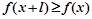 ,則稱
,則稱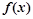 為M上的l高調函數.對于定義域為R的奇函數
為M上的l高調函數.對于定義域為R的奇函數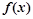 ,當
,當 ,若
,若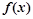 為R上的4高調函數,則實數a的取值范圍為________
為R上的4高調函數,則實數a的取值范圍為________查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com