
已知函數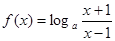
 .
.
(1)判斷函數 的奇偶性;
的奇偶性;
(2)判斷函數 在
在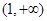 上的單調性,并給出證明;
上的單調性,并給出證明;
(3)當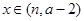 時,函數
時,函數 的值域是
的值域是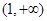 ,求實數
,求實數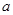 與
與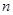 的值;
的值;
 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:解答題
已知函數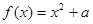 .
.
(1)若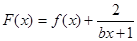 是偶函數,在定義域上
是偶函數,在定義域上 恒成立,求實數
恒成立,求實數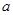 的取值范圍;
的取值范圍;
(2)當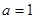 時,令
時,令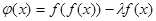 ,問是否存在實數
,問是否存在實數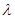 ,使
,使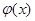 在
在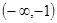 上是減函數,在
上是減函數,在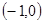 上是增函數?如果存在,求出
上是增函數?如果存在,求出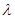 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com