
在△ABC中,點B(-6,0)、C(0,8),且sinB、sinA、sinC成等差數列.
(1)求證:頂點A在一個橢圓上運動.
(2)指出這個橢圓的焦點坐標以及焦距.
|
解:(1)證明:由題意得sinB+sinC=2sinA,由正弦定理,得sinB= (2)這個橢圓的焦點坐標分別是(-6,0)、(0,8),焦距是10. 解析:本題依據等差數列的定義以及結合正弦定理將已知轉化為相應的邊間的關系,再利用橢圓的定義將問題解決. |
|
有關證明或判定動點的軌跡是橢圓這樣的問題,可以緊緊圍繞著相應的橢圓的定義,去探尋相應的動點到某兩個定點的距離的和等于一個常數,并且注意這個常數與這兩個定點之間的距離的大小關系,從而確定. |


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| CF |
| CG |
查看答案和解析>>
科目:高中數學 來源:設計選修數學-1-1蘇教版 蘇教版 題型:044
在△ABC中,點B(-6,0)、C(0,8),且sinB,sinA,sinC成等差數列.
(1)求證:頂點A在一個橢圓上運動.
(2)指出這個橢圓的焦點坐標以及焦距.
查看答案和解析>>
科目:高中數學 來源:江蘇期中題 題型:解答題
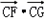 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南京27中高三(上)學情分析數學試卷(08)(解析版) 題型:解答題
 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com