
 的取值范圍.
的取值范圍. =
= ,再由二次函數的性質求得
,再由二次函數的性質求得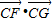 的最大值和最小值,
的最大值和最小值,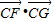 的取值范圍.
的取值范圍. ,解之得:
,解之得: ,∴A(-2,-8),
,∴A(-2,-8), ,即 7x-6y-34=0.
,即 7x-6y-34=0. 解得
解得 ,即C(4,-1),又 圓心M(0,-1),
,即C(4,-1),又 圓心M(0,-1), =
= =(16-r2)cos2∠CFM=(16-r2)(1-2sin2∠GCM)=
=(16-r2)cos2∠CFM=(16-r2)(1-2sin2∠GCM)= ,
, =
= ,
, =
= .
. 的取值范圍為
的取值范圍為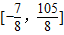 .
.

科目:高中數學 來源: 題型:
| CF |
| CG |
查看答案和解析>>
科目:高中數學 來源:設計選修數學-1-1蘇教版 蘇教版 題型:044
在△ABC中,點B(-6,0)、C(0,8),且sinB,sinA,sinC成等差數列.
(1)求證:頂點A在一個橢圓上運動.
(2)指出這個橢圓的焦點坐標以及焦距.
查看答案和解析>>
科目:高中數學 來源:選修設計數學1-1北師大版 北師大版 題型:044
在△ABC中,點B(-6,0)、C(0,8),且sinB、sinA、sinC成等差數列.
(1)求證:頂點A在一個橢圓上運動.
(2)指出這個橢圓的焦點坐標以及焦距.
查看答案和解析>>
科目:高中數學 來源:江蘇期中題 題型:解答題
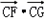 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com