如下圖,已知平行六面體ABCD—A1B1C1D1中,底面ABCD是邊長為a的正方形,側(cè)棱AA1長為b,且AA1與AB、AD的夾角都是120°.
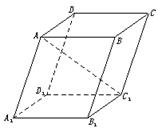
求:(1)AC1的長;
(2)直線BD1與AC所成的角的余弦值.
(1)
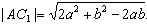
(2)
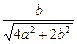
命題意圖:本題主要考查利用向量法來解決立體幾何問題,屬★★★★★級題目.
知識依托:向量的加、減及向量的數(shù)量積.
錯解分析:注意<
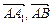
>=<
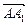
,
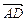
>=120°而不是60°,<
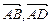
>=90°.
技巧與方法:數(shù)量積公式及向量、模公式的巧用、變形用.
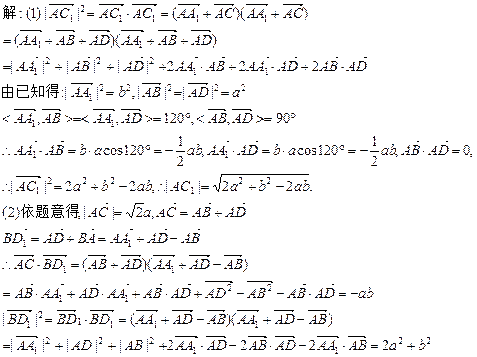

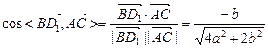
∴BD1與AC所成角的余弦值為
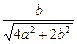
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
把正方形
ABCD沿對角線
AC折起成直二面角,點
E、
F分別是
AD、
BC的中點,點
O是原正方形的中心,求:

(1)
EF的長;
(2)折起后∠
EOF的大小.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
.將銳角A為60°,邊長為
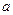
的菱形ABCD沿對角線BD折成60°的二面角,則AC與BD的中點O的距離為( )。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
一個無蓋的正方體盒子展開后的平面圖如圖所示,
A、
B、
C是展開圖上的三點,則在正方體盒子中,∠
ABC的度數(shù)是多少?

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,
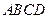
是直角梯形,角DABS是直角,
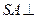
面
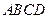
,
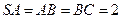
,
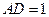
,求面
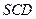
和面
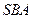
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,已知二面角
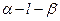
,
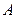
,
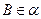
.
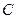
,
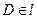
,四邊形
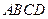
為矩形,
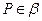
,
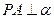
,且
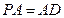
,
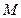
,
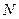
依次是
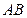
,
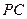
的中點.
(1) 求二面角
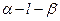
的大小;
(2) 求證:
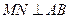
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
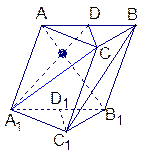
已知斜三棱柱
ABC—
A1B1C1中,
A1C1=
B1C1=2,
D、
D1分別是
AB、
A1B1的中點,平面
A1ABB1⊥平面
A1B1C1,異面直線
AB1和
C1B互相垂直.
(1)求證:
AB1⊥
C1D1;
(2)求證:
AB1⊥面
A1CD;
(3)若
AB1=3,求直線
AC與平面
A1CD所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
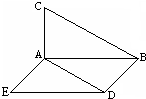
如圖∠BAC=90°,等腰直角三角形ABC所在的平面與正方形ABDE所在的平面互相垂直,則異面直線AD與BC所成角的大小是_______.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在長方體
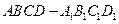
中,
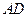
=
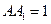
,

,點
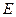
為棱
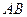
的中點,則二面角
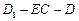
的大小為
(結(jié)果用反三角函數(shù)值表示)
查看答案和解析>>


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案
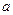 的菱形ABCD沿對角線BD折成60°的二面角,則AC與BD的中點O的距離為( )。
的菱形ABCD沿對角線BD折成60°的二面角,則AC與BD的中點O的距離為( )。





