
如圖,在直棱柱ABC—A1B1C1中,AC=BC=2,∠ACB=90º,AA1=2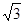 ,E,F(xiàn)分別為AB、CB中點,過直線EF作棱柱的截面,若截面與平面ABC所成的二面角的大小為60º,則截面的面積為( ).
,E,F(xiàn)分別為AB、CB中點,過直線EF作棱柱的截面,若截面與平面ABC所成的二面角的大小為60º,則截面的面積為( ).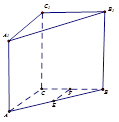
A.3或1 B.1 C.4或1 D.3或4
A
解析試題分析:根據(jù)截面與平面ABC所成的二面角的大小為60°,故需要分類討論,利用截面為梯形,可以計算各邊長,從而可求截面的面積.解:解:由題意,分類討論:如右圖,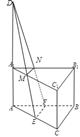
截面為MNFE,延長EM,CN,AA1,交于點D,∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分別是AC、AB的中點,∴DE⊥EF,∴∠AED為截面與平面ABC所成的二面角,∴∠AED=60°,∵AE= AC=1,∴DE=2∵EF=
AC=1,∴DE=2∵EF=
BC=1∴S△DEF= ×2×1=1,∵DA=6
×2×1=1,∵DA=6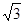 ,∴DA1=
,∴DA1= DA∴SDMN=
DA∴SDMN=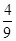 S△DEF=
S△DEF=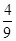 ,∴截面的面積為1
,∴截面的面積為1
設(shè)截面EFN'M'在底面中的射影為EFPQ,則EF=1,M'Q=2,CE=1,∠M'EQ=60°,∴EQ=
∴PQ=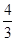 ∴射影EFPQ的面積為
∴射影EFPQ的面積為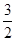 ,∵截面與平面ABC所成的二面角的大小為60°,∴截面EFN'M'的面積為
,∵截面與平面ABC所成的二面角的大小為60°,∴截面EFN'M'的面積為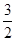 ÷cos60°=3故答案為A
÷cos60°=3故答案為A
考點:截面面積
點評:本題以直三棱柱為載體,考查截面面積的計算,搞清截面圖形是解題的關(guān)鍵.


科目:高中數(shù)學 來源: 題型:單選題
設(shè)m,n是兩條不同直線,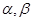 是兩個不同的平面,給出下列四個命題
是兩個不同的平面,給出下列四個命題
①若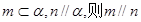 ②
②
③若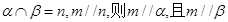 ④若
④若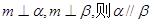
其中正確的命題是 ( )
| A.① | B.② | C.③④ | D.②④ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
已知長方體ABCD—A1B1ClD1內(nèi)接于球O,底面ABCD是邊長為2的正方形,E為AA1的中點,OA⊥平面BDE,則球O的表面積為
A.8 | B.16 : : | C.14 | D.18 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
如圖,四面體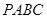 的六條邊均相等,
的六條邊均相等,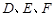 分別是
分別是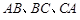 的中點,則下列四個結(jié)論中不成立的是 ( )
的中點,則下列四個結(jié)論中不成立的是 ( ) 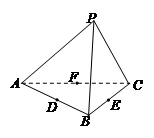
A.平面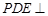 平面 平面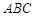 | B.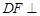 平面 平面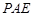 |
C. //平面 //平面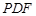 | D.平面 平面 平面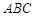 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
在棱長為1的正方體ABCD—A1B1C1D1中,M和N分別為A1B1和BB1的中點,那么直線AM與CN所成角的余弦值是 ( )
A.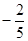 | B.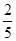 | C.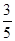 | D.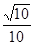 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
如圖,平面α⊥平面β,A∈α,B∈β,AB與平面α所成的角為 ,過A、B分別作兩平面交線的垂線,垂足為A′、B′,若
,過A、B分別作兩平面交線的垂線,垂足為A′、B′,若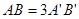 ,則AB與平面β所成的角的正弦值是( )
,則AB與平面β所成的角的正弦值是( )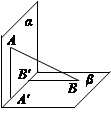
A.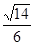 | B.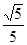 | C.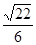 | D.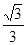 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
設(shè) 是平面
是平面 內(nèi)的一條定直線,
內(nèi)的一條定直線, 是平面
是平面 外的一個定點,動直線
外的一個定點,動直線 經(jīng)過點
經(jīng)過點 且與
且與 成
成 角,則直線
角,則直線 與平面
與平面 的交點
的交點 的軌跡是
的軌跡是
| A.圓 | B.橢圓 | C.雙曲線 | D.拋物線 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
已知 是直線,
是直線, 是平面,給出下列命題:
是平面,給出下列命題:
①若 ,
, ,
, ,則
,則 或
或 .
.
②若 ,
, ,
, ,則
,則 .
.
③若m
 ,n
,n
 ,m∥
,m∥ ,n∥
,n∥ ,則
,則 ∥
∥
④若 ,
, 且
且 ,
, ,則
,則
其中正確的命題是( )。
| A.①② | B.②④ | C.②③ | D.③④ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
在三棱錐P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分別是棱AB、BC、CP的中點,AB=AC=1,PA=2,則直線PA與平面DEF所成角的正弦值為( )
A.  B.
B.  C.
C. 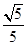 D.
D. 
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com