
已知函數
(1)判斷函數 的奇偶性;
的奇偶性;
(2)試用函數單調性定義說明函數 在區間
在區間 和
和 上的增減性;
上的增減性;
(3)若 滿足:
滿足: ,試證明:
,試證明: .
.
(1)偶函數,(2)在 上是減函數,在
上是減函數,在 上是增函數(3)詳見解析.
上是增函數(3)詳見解析.
解析試題分析:(1)判定函數奇偶性,首先判定函數定義域是否關于原點對稱,然后再判斷 與
與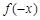 的相等或相反關系.本題定義域為一切實數,關于原點對稱.函數
的相等或相反關系.本題定義域為一切實數,關于原點對稱.函數 為分段函數,需分類討論. 當
為分段函數,需分類討論. 當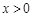 時,
時, ,
,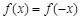 .當
.當 時,
時,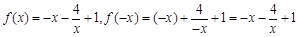 ,
,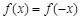 .故
.故 為偶函數.(2)利用定義研究函數單調性,需注重作差后的變形,關鍵是提取公因式,進行因式分解,以便判斷符號.(3)由于
為偶函數.(2)利用定義研究函數單調性,需注重作差后的變形,關鍵是提取公因式,進行因式分解,以便判斷符號.(3)由于 是同區間的兩個任意數,所以只需證
是同區間的兩個任意數,所以只需證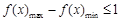 ,從而本題實質為求函數最值.由函數奇偶性及單調性知:
,從而本題實質為求函數最值.由函數奇偶性及單調性知: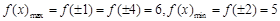 ,所以
,所以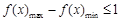 成立.
成立.
試題解析:解:(1)∵當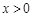 時,
時,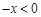 ,∴
,∴
∴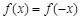 2分
2分
∵當 時,
時, ,∴
,∴
∴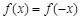 4分
4分
∴對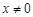 都有
都有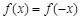 ,故
,故 為偶函數 5分
為偶函數 5分
(2)當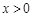 時,
時,
設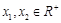 且
且 ,則
,則 7分
7分
∴當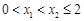 時,
時,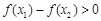 即
即
當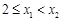 時,
時,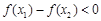 即
即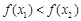 9分
9分
∴函數 在區間
在區間 上是減函數,在區間
上是減函數,在區間 上是增函數 11分
上是增函數 11分
(3)由(2)可知,當 時:
時:
若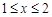 ,則
,則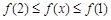 即
即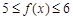
若 ,則
,則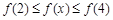 即
即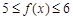
∴當 時,有
時,有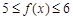 12分
12分
又由(1)可知 為偶函數,∴當
為偶函數,∴當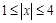 時,有
時,有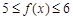 13分
13分
∴若 ,
,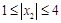 時,則
時,則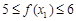 ,
,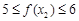 14分
14分
∴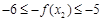 ,
, 即
即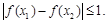 15分
15分
考點:分段函數的奇偶性、單調性.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:解答題
已知 (
( )
)
(1)若方程 有3個不同的根,求實數
有3個不同的根,求實數 的取值范圍;
的取值范圍;
(2)在(1)的條件下,是否存在實數 ,使得
,使得 在
在 上恰有兩個極值點
上恰有兩個極值點 ,且滿足
,且滿足 ,若存在,求實數
,若存在,求實數 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓 (a>b>0)的左焦為F,右頂點為A,上頂點為B,O為坐標原點,M為橢圓上任意一點,過F,B,A三點的圓的圓心為(p,q).
(a>b>0)的左焦為F,右頂點為A,上頂點為B,O為坐標原點,M為橢圓上任意一點,過F,B,A三點的圓的圓心為(p,q).
(1).當p+q≤0時,求橢圓的離心率的取值范圍;
(2).若D(b+1,0),在(1)的條件下,當橢圓的離心率最小時, 的最小值為
的最小值為 ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
判斷下列對應是否是從集合A到集合B的函數.
(1) A=B=N*,對應法則f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,對應法則f:x→y,這里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],對應法則f:x→y,這里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,對應法則:對任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 對任意的
對任意的 恒有
恒有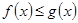 成立.
成立.
(1)記 如果
如果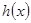 為奇函數,求b,c滿足的條件;
為奇函數,求b,c滿足的條件;
(2)當b=0時,記 若
若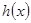 在
在 )上為增函數,求c的取值范圍;
)上為增函數,求c的取值范圍;
(3)證明:當 時,
時, 成立;
成立;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)對于任意x,y∈R,總有f(x)+f(y)=f(x+y),且當x>0時,f(x)<0,f(1)=- .
.
(1)求證:f(x)在R上是減函數.
(2)求f(x)在[-3,3]上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com