Question

（2012•鷹潭一模）已知命題：
（1）函數y=2sinx的圖象向右平移

π

6

個單位后得到函數y=2sin(x+

π

6

)的圖象；
（2）已知f(x)=

x+3，(x≤1) -x2+2x+3，(x＞1)

，則函數g（x）=f（x）-e^x的零點個數為2；
（3）函數y=log

1

2

(x2-5x+6)的單調增區間為(-∞，

5

2

)．
則以上命題中真命題個數為（　　）

A．0

B．3

C．2

D．1

Answer 1

分析：（1）函數y=2sinx的圖象向右平移

π

6

個單位后得到函數y=sin（x-

π

6

）的圖象；（2）分別作出函數y=f（x），y=e^x的圖象，結合函數的圖象可求y=f（x）與y=e^x的圖象交點個數，（3）先求函數的定義域，然后由復合函數的單調區間的求解方法可求

解答：解：（1）函數y=2sinx的圖象向右平移

π

6

個單位后得到函數y=sin（x-

π

6

）的圖象；故（1）錯誤
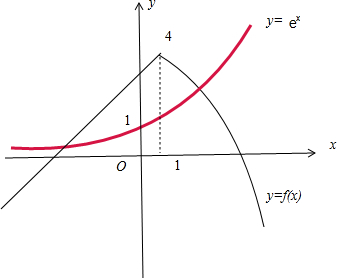
（2）分別作出函數y=f（x），y=e^x的圖象，結合函數的圖象可知y=f（x）與y=e^x的圖象有2個交點，函數g（x）=f（x）-e^x的零點個數為2；故（2）正確

（3）由題意可得，函數的定義域為x＞3或x＜2
令t（x）=x²-5x+6，f（t）=log

1

2

t(x)，由復合函數的單調性可知，函數y=log

1

2

(x2-5x+6)的單調增區間即為t（x）=x²-5x+6的單調遞減區間（-∞，2）；故（3）錯誤
故正確的為（2）
故選D

點評：本題主要考查了三角函數的圖象的平移，函數的零點個數的判斷，及復合函數的單調區間的求解等函數知識的綜合應用，屬于綜合性試題