下面是一段演繹推理：
如果直線平行于平面，則這條直線平行于平面內的所有直線；
已知直線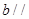
平面
，直線
平面；
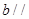所以直線直線
，在這個推理中（ ）
| A．大前提正確，結論錯誤 |
| B．小前提與結論都是錯誤的 |
| C．大、小前提正確，只有結論錯誤 |
| D．大前提錯誤，結論錯誤 |
閱讀快車系列答案科目：高中數學 來源： 題型：單選題
用反證法證明命題：若整數系數的一元二次方程
有有理實數根，那么
，
，
中至少有一個是偶數，下列假設中正確的是（ ）
| A．假設，，都是偶數 |
| B．假設，，都不是偶數 |
| C．假設，，至多有一個是偶數 |
| D．假設，，至多有兩個偶數 |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
用反證法證明命題：“一個三角形中不能有兩個直角”的過程歸納為以下三個步驟：
①
，這與三角形內角和為
相矛盾，
不成立；②所以一個三角形中不能有兩個直角；③假設三角形的三個內角
、
、
中有兩個直角，不妨設，正確順序的序號為
| A．①②③ | B．③①② | C．①③② | D．②③① |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
圓周上2個點可連成1條弦,這條弦可將圓面劃分成2部分;圓周上3個點可連成3條弦,這3條弦可將圓面劃分成4部分;圓周上4個點可連成6條弦,這6條弦最多可將圓面劃分成8部分.則這些弦最多可把圓面分成 ( ) 部分
| A．2n-1 | B．2n | C．2n+1 | D．2n+2 |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
用數學歸納法證明“n3＋(n＋1)3＋(n＋2)3，(n∈N＋)能被9整除”，要利
用歸納法假設證n＝k＋1時的情況，只需展開( )．
| A．(k＋3)3 | B．(k＋2)3 |
| C．(k＋1)3 | D．(k＋1)3＋(k＋2)3 |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
如圖,模塊①～⑤均由4個棱長為1的小正方體構成,模塊⑥由15個棱長為1的小正方體構成.現從模塊①～⑤中選出三個放到模塊⑥上,使得模塊⑥成為一個棱長為3的大正方體,則下列選擇方案中,能夠完成任務的為( )
| A．模塊①,②,⑤ | B．模塊①,③,⑤ |
| C．模塊②,④,⑤ | D．模塊③,④,⑤ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
與直線
