
�����}�M��10�֣����p����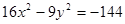 �Ľ��c(di��n)����(bi��o)���x���ʺ͝u��������.
�Ľ��c(di��n)����(bi��o)���x���ʺ͝u��������.
���c(di��n)����(bi��o)�飺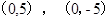 ���x���ʞ飺
���x���ʞ飺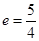 ,�u�������̞飺
,�u�������̞飺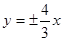 .
.
����ԇ�}������������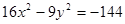 �����(bi��o)��(zh��n)����
�����(bi��o)��(zh��n)����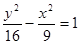 ��
��
�ã�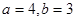 ,
,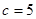 �� ����4��
�� ����4��
���Խ��c(di��n)����(bi��o)�飺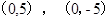 �� ����6��
�� ����6��
�x���ʞ飺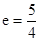 ����8��
����8��
�u�������̞飺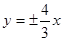 . ����10��
. ����10��
���c(di��n)����С�}��Ҫ�������p�����Ę�(bi��o)��(zh��n)�������c(di��n)���x���ʡ��u�����Ȼ�����������W(xu��)�������A(ch��)֪�R�����պ�Ӌ(j��)������.
�c(di��n)�u�����p�����Ę�(bi��o)��(zh��n)������������P(gu��n)�I�Ƿ��役�c(di��n)���Ă�(g��)����(bi��o)�S�ϣ�����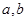 .
.


 �_�Ŀ옷�������I(y��)������I(y��)����������ϵ�д�
�_�Ŀ옷�������I(y��)������I(y��)����������ϵ�д� ���}Ӗ(x��n)��ϵ�д�
���}Ӗ(x��n)��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A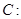
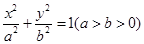 ���x���ʞ�
���x���ʞ�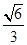 ���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
������E�A �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��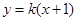 �c�E�A
�c�E�A �ཻ��
�ཻ�� ��
�� ���c(di��n). ��������
���c(di��n). ��������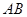 ���c(di��n)��
���c(di��n)��
�M����(bi��o)��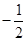 �����
����б��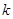 ��ֵ�������c(di��n)
��ֵ�������c(di��n)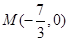 �����C��
�����C��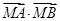 �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��12�֣���֪���タ ��
��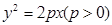 �^�c(di��n)
�^�c(di��n)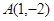 .��1�����タ
.��1�����タ �ķ��̣��������(zh��n)�����̣�
�ķ��̣��������(zh��n)�����̣�
��2���Ƿ����ƽ����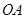 ��
�� ������(bi��o)ԭ�c(di��n)����ֱ��
������(bi��o)ԭ�c(di��n)����ֱ��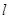 ��ʹ��ֱ��
��ʹ��ֱ��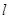 �c���タ
�c���タ �й����c(di��n)����ֱ��
�й����c(di��n)����ֱ��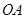 �c
�c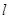 ��
��
���x����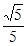 �������ڣ����ֱ��
�������ڣ����ֱ��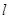 �ķ��̣��������ڣ��f������.
�ķ��̣��������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
ij���タ�ι�������20�ף�����4�ף��ڽ���r(sh��)ÿ��4������һ֧��֧�Σ����������L��֧�����L. 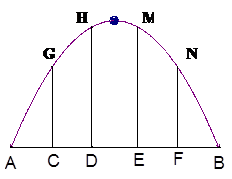
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��12�֣���֪�E�A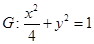 ���^�c(di��n)��m,0�����A
���^�c(di��n)��m,0�����A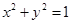 ���о�
���о�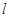 ���E�AG��A��B���c(di��n).
���E�AG��A��B���c(di��n).
��1����E�AG�Ľ��c(di��n)����(bi��o)���x���ʣ�
��2����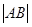 ��ʾ��m�ĺ���(sh��)������
��ʾ��m�ĺ���(sh��)������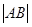 �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(��С�}15��)�O(sh��)���タ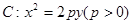 ���c(di��n)
���c(di��n)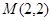 ,.б�ʞ�
,.б�ʞ�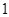 ��ֱ���c���タ
��ֱ���c���タ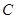 �ཻ��ͬ�ăɂ�(g��)�c(di��n)
�ཻ��ͬ�ăɂ�(g��)�c(di��n)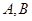 .���c(di��n)
.���c(di��n)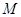 ǡ�Þ�
ǡ�Þ�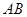 �����c(di��n).
�����c(di��n).
(1)���タ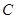 �ķ���,
�ķ���,
(2) ���タ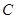 ���Ƿ���ڮ���
���Ƿ���ڮ���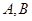 ���c(di��n)
���c(di��n)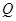 ,ʹ�ý�(j��ng)�^�c(di��n)
,ʹ�ý�(j��ng)�^�c(di��n)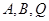 �ĈA�͒��タ
�ĈA�͒��タ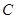 ��
��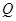 ̎����ͬ���о�.������,����c(di��n)
̎����ͬ���о�.������,����c(di��n)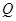 ������(bi��o);��������,Ո�f������.
������(bi��o);��������,Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��14�֣������ƣ���֪�E�A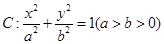 ���^���c(di��n)�Ҵ�ֱ���L�S�����L��1���ҽ��c(di��n)�c���S�ɶ��c(di��n)��(g��u)�ɵ�߅������.
���^���c(di��n)�Ҵ�ֱ���L�S�����L��1���ҽ��c(di��n)�c���S�ɶ��c(di��n)��(g��u)�ɵ�߅������.
��1����E�A�ķ��̣�
��2���^�c(di��n)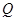
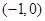 ��ֱ��
��ֱ�� ���E�A��
���E�A�� ���c(di��n)����ֱ��
���c(di��n)����ֱ��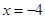 ���c(di��n)
���c(di��n)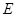 ����
����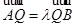 ,
, ,
,
���C��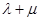 �鶨ֵ����Ӌ(j��)���ԓ��ֵ.
�鶨ֵ����Ӌ(j��)���ԓ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��13�֣� ��֪���タ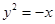 �cֱ��
�cֱ��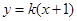 �ཻ��
�ཻ�� ���c(di��n).
���c(di��n).
��1�����C���� ��ֱ���ĈA�^����(bi��o)ϵ��ԭ�c(di��n)
��ֱ���ĈA�^����(bi��o)ϵ��ԭ�c(di��n) ����2����(d��ng)
����2����(d��ng)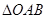 ����e����
����e����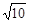 �r(sh��)����
�r(sh��)���� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��14�֣���֪�L���� ��
��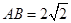 ��
��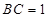 ����
���� �����c(di��n)
�����c(di��n)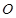 ��
��
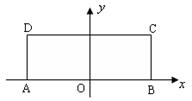
ԭ�c(di��n)������D��ʾ��ƽ��ֱ������(bi��o)ϵ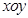 .
.
(1)����A��B�齹�c(di��n)�����^C��D���c(di��n)�ęE�A�Ę�(bi��o)��(zh��n)����;
(2)�O(sh��)�E�A������һ�c(di��n)��P����x�S����һ��(g��)��(d��ng)�c(di��n)Q��t��0��������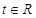 ��̽��
��̽��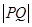 ����
����
Сֵ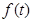 ��
��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com