
�O(sh��)����(sh��)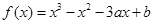 .
.
��1��������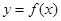 ���c(di��n)
���c(di��n)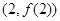 ̎�cֱ��
̎�cֱ��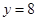 ���У���a��b��ֵ��
���У���a��b��ֵ��
��2����(sh��) ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��1��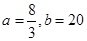 ����2��
����2��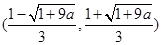 .
.
����ԇ�}��������1�����Ȍ�(du��)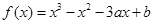 ��(d��o)����
��(d��o)����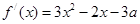 �����Ì�(d��o)��(sh��)�Ď����x��������c(di��n)�����x�ɵ�
�����Ì�(d��o)��(sh��)�Ď����x��������c(di��n)�����x�ɵ� ���ɵ�
���ɵ� �����ɽ��a��b����2������(j��)
�����ɽ��a��b����2������(j��)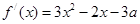 ���ͷ���
���ͷ���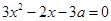 �Ƿ��н⣬����
�Ƿ��н⣬����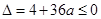 ��
��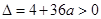 չ�_ӑՓ���ó����{(di��o)�^(q��)�g.
չ�_ӑՓ���ó����{(di��o)�^(q��)�g.
�⣺��1����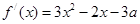
��?y��n)�����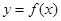 ���c(di��n)
���c(di��n)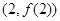 ̎�cֱ��
̎�cֱ��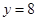 ���У�
����
�� ����2�֣���
����2�֣��� ���
���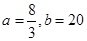 �� ��6��
�� ��6��
��2����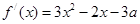
��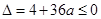 ����
���� ��
�� ��
��
����(sh��) ��(���ޣ�����)�φ��{(di��o)�f����8�֣�
��(���ޣ�����)�φ��{(di��o)�f����8�֣�
��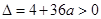 ����
���� ���˕r(sh��)
���˕r(sh��)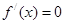 �ăɂ�(g��)����
�ăɂ�(g��)����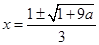
��(d��ng)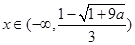 ��
�� �r(sh��)
�r(sh��)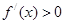
��(d��ng) �r(sh��)��
�r(sh��)�� ��11�֣�
��11�֣�
�� �r(sh��)�������^(q��)�g�鮔(d��ng)
�r(sh��)�������^(q��)�g�鮔(d��ng) ��
��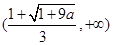
�Μp�^(q��)�g��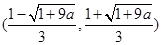 ��13�֣�
��13�֣�
���c(di��n)��1.��(d��o)��(sh��)�Ď����x��2.��(d��o)��(sh��)�о�����(sh��)�Ć��{(di��o)��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)����(sh��) .
.
��1���� ��
�� �r(sh��)�ИOֵ����(sh��)��(sh��)
�r(sh��)�ИOֵ����(sh��)��(sh��) ��ֵ��
��ֵ�� �ĘO��ֵ��
�ĘO��ֵ��
��2���� �ڶ��x������������(sh��),��(sh��)��(sh��)
�ڶ��x������������(sh��),��(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)����(sh��)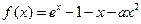 ��
��
��1����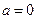 ����
���� ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2������(d��ng)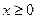 �r(sh��)��
�r(sh��)��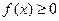 ����a��ȡֵ������
����a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��) ��
��
��1�������� ���c(di��n)
���c(di��n) ̎���о����̞�
̎���о����̞� ����
���� ��ֵ��
��ֵ��
��2����(d��ng) �r(sh��)����
�r(sh��)���� �Ć��{(di��o)�^(q��)�g�c�Oֵ��
�Ć��{(di��o)�^(q��)�g�c�Oֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪����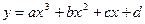 �M�����Зl����
�M�����Зl����
���^ԭ�c(di��n)������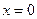 ̎��(d��o)��(sh��)�飭1������
̎��(d��o)��(sh��)�飭1������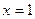 ̎�о����̞�
̎�о����̞�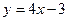 .
.
(1) ��(sh��)��(sh��)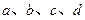 ��ֵ��
��ֵ��
��2����(sh��)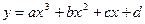 �ĘOֵ.
�ĘOֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
������(sh��)y��f(x)��x��x0̎ȡ�ØO��ֵ��OСֵ���t�Qx0�麯��(sh��)y��f(x)�ĘOֵ�c(di��n)����֪A��b�nj�(sh��)��(sh��)��1�ͣ�1�Ǻ���(sh��)f(x)��x3��Ax2��b x�ăɂ�(g��)�Oֵ�c(di��n)��
(1)��A��b��ֵ��
(2)�O(sh��)����(sh��)g(x)�Č�(d��o)����(sh��)g��(x)��f(x)��2����g(x)�ĘOֵ�c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����(sh��)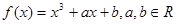 �ĈD��ӛ��E.�^�c(di��n)
�ĈD��ӛ��E.�^�c(di��n)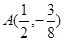 ������E���о����@�ӵ��о����҃H�Ѓɗl����
������E���о����@�ӵ��о����҃H�Ѓɗl����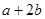 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪����(sh��) ��
��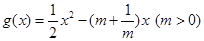 ����
����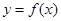 ���c(di��n)
���c(di��n)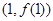 ̎���о����̞�
̎���о����̞�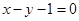 .
.
��1����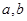 ��ֵ��
��ֵ��
��2��������(sh��)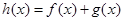 �څ^(q��)�g
�څ^(q��)�g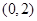 ��(n��i)���҃H��һ��(g��)�Oֵ�c(di��n)����
��(n��i)���҃H��һ��(g��)�Oֵ�c(di��n)����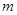 ��ȡֵ������
��ȡֵ������
��3���O(sh��)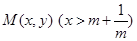 �������
�������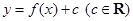 ��
��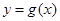 �Ľ��c(di��n)���҃������ڽ��c(di��n)
�Ľ��c(di��n)���҃������ڽ��c(di��n)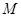 ̎���о��քe��
̎���о��քe��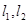 .��ȡ
.��ȡ ��ԇ�Дஔ(d��ng)ֱ��
��ԇ�Дஔ(d��ng)ֱ��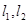 �c
�c �S���ɵ��������Εr(sh��)
�S���ɵ��������Εr(sh��)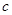 ֵ�Ă�(g��)��(sh��)���f������.
ֵ�Ă�(g��)��(sh��)���f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)����(sh��)f(x)��2x3��3(a��1)x2��1������a��1����(sh��)f(x)�Ć��{(di��o)�^(q��)�g�͘Oֵ��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com