
已知數列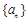 滿足
滿足 .
.
(1)證明數列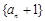 為等比數列,并求出數列
為等比數列,并求出數列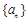 的通項公式;
的通項公式;
(2)若數列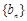 滿足
滿足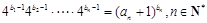 .證明:數列
.證明:數列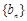 是等差數列.
是等差數列.
(3)證明: .
.
(1)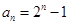 ;(2)詳見解析;(3)詳見解析.
;(2)詳見解析;(3)詳見解析.
解析試題分析:(1)證明數列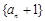 為等比數列,就是證明
為等比數列,就是證明 為一個常數. 因為
為一個常數. 因為 ,所以
,所以 ,所以,
,所以,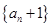 是以2為首項,2為公比的等比數列. 則
是以2為首項,2為公比的等比數列. 則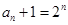 ,即
,即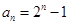 ,
,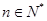 ;(2)證明數列
;(2)證明數列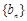 是等差數列,就是要證明
是等差數列,就是要證明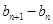 為一個常數.首先化簡等式
為一個常數.首先化簡等式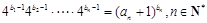 ,即
,即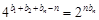 ,所以
,所以 ,這實質是
,這實質是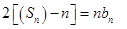 ,因此作差消去
,因此作差消去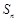 得:
得: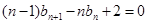 ,再作差消去常數得:
,再作差消去常數得: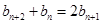 ,
,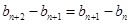 ,即
,即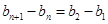 ;(3)證明數列不等式,一般有兩個思路,一是求和,二是放縮.本題由于通項
;(3)證明數列不等式,一般有兩個思路,一是求和,二是放縮.本題由于通項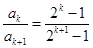 不適宜求和,所以嘗試放縮,即利用變量分離進行放縮,由
不適宜求和,所以嘗試放縮,即利用變量分離進行放縮,由 ,得
,得 .
.
試題解析:(1)因為 ,所以
,所以 ,且
,且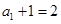 ,
,
所以,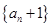 是以2為首項,2為公比的等比數列. 2分
是以2為首項,2為公比的等比數列. 2分
則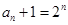 ,即
,即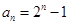 ,
,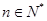 . 3分
. 3分
(2)因為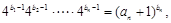 所以.
所以.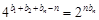 4分
4分
所以 ①
①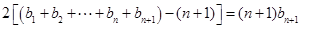 ② 6分
② 6分
②-①,得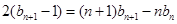
即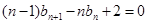 ③
③ 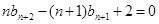 ④ 8分
④ 8分
④-③,得 ,
,
即 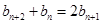
得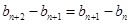 ,
,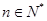 10分
10分
所以數列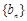 為等差數列.
為等差數列.
(3)因為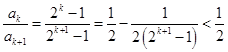 ,
, 11分
11分
所以 . 12分
. 12分
考點:用定義證明等差數列、等比數列,放縮法證明數列不等式


科目:高中數學 來源: 題型:解答題
已知函數f(x)= ,數列{an}滿足:2an+1-2an+an+1an=0且an≠0.數列{bn}中,b1=f(0)且bn=f(an-1).
,數列{an}滿足:2an+1-2an+an+1an=0且an≠0.數列{bn}中,b1=f(0)且bn=f(an-1).
(1)求證:數列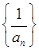 是等差數列;
是等差數列;
(2)求數列{|bn|}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列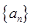 ,
,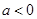 滿足
滿足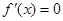 ,
,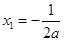 ,
,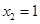 ,
,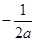 .
.
(1)求證:數列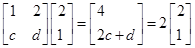 是等差數列,并求數列
是等差數列,并求數列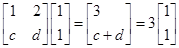 的通項公式;
的通項公式;
(2)設數列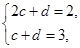 滿足
滿足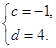 ,對于任意給定的正整數
,對于任意給定的正整數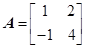 ,是否存在正整數
,是否存在正整數 ,
, (
(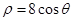 ),使得
),使得 ,
,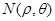 ,
,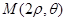 成等差數列?若存在,試用
成等差數列?若存在,試用 表示
表示 ,
,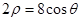 ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個三角形數表按如下方式構成(如圖:其中項數 ):第一行是以4為首項,4為公差的等差數列,從第二行起,每一個數是其肩上兩個數的和,例如:
):第一行是以4為首項,4為公差的等差數列,從第二行起,每一個數是其肩上兩個數的和,例如: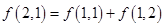 ;
;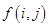 為數表中第
為數表中第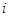 行的第
行的第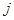 個數.
個數.
求第2行和第3行的通項公式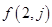 和
和 ;
;
證明:數表中除最后2行外每一行的數都依次成等差數列,并求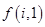 關于
關于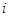 (
(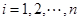 )的表達式;
)的表達式;
(3)若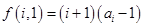 ,
,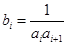 ,試求一個等比數列
,試求一個等比數列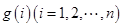 ,使得
,使得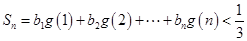 ,且對于任意的
,且對于任意的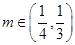 ,均存在實數
,均存在實數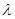 ?,當
?,當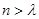 時,都有
時,都有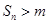 .
.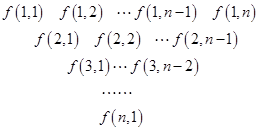
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列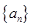 中,
中,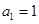 ,對任意的
,對任意的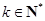 ,
,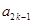 、
、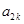 、
、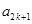 成等比數列,公比為
成等比數列,公比為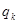 ;
;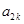 、
、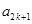 、
、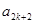 成等差數列,公差為
成等差數列,公差為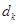 ,且
,且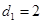 .
.
(1)寫出數列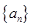 的前四項;
的前四項;
(2)設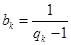 ,求數列
,求數列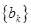 的通項公式;
的通項公式;
(3)求數列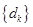 的前
的前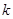 項和
項和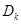 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
正實數數列{an}中,a1=1,a2=5,且{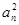 }成等差數列.
}成等差數列.
(1)證明:數列{an}中有無窮多項為無理數;
(2)當n為何值時,an為整數?并求出使an<200的所有整數項的和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com