
已知 ,
,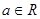
(Ⅰ)當 時,求曲線
時,求曲線 在點
在點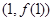 處的切線方程;
處的切線方程;
(Ⅱ)若 在
在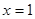 處有極值,求
處有極值,求 的單調遞增區間;
的單調遞增區間;
(Ⅲ)是否存在實數 ,使
,使 在區間
在區間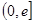 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(Ⅰ) (Ⅱ)
(Ⅱ)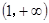 (Ⅲ)
(Ⅲ)
解析試題分析:(Ⅰ)求曲線在一點處的切線方程,一要抓切點(1,2),一要抓導數的幾何意義即切線的斜率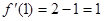 ,便求出切線方程
,便求出切線方程 ;(Ⅱ)先利用極值求出系數
;(Ⅱ)先利用極值求出系數 ,再利用
,再利用 及定義域
及定義域 ,求出單調遞增區間為
,求出單調遞增區間為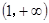 ;(Ⅲ)利用導數求某區間上的最值,要綜合應用極值、單調性進行判定求解,特別對
;(Ⅲ)利用導數求某區間上的最值,要綜合應用極值、單調性進行判定求解,特別對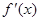 的形式、
的形式、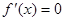 的根進行分類討論.多見于單調函數、單峰(谷)函數.
的根進行分類討論.多見于單調函數、單峰(谷)函數.
試題解析:(Ⅰ)函數 的定義域為
的定義域為 , 因為
, 因為 ,所以
,所以
當 時,
時,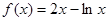 ,
, ,所以
,所以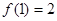 ,
,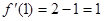
所以曲線 在點
在點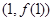 處的切線方程為
處的切線方程為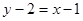 ,即
,即 . 3分
. 3分
(Ⅱ)因為 在
在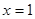 處有極值,所以
處有極值,所以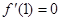 , 由(Ⅰ)知
, 由(Ⅰ)知 ,所以
,所以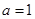
經檢驗,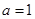 時
時 在
在 處有極值. 4分
處有極值. 4分
所以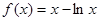 ,令
,令 ,解得
,解得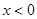 或
或 ;
;
因為 的定義域為
的定義域為 ,所以
,所以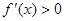 的解集為
的解集為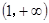 ,
,
即 的單調遞增區間為
的單調遞增區間為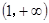 . 6分
. 6分
(Ⅲ)假設存在實數 ,使
,使 在區間
在區間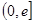 上有最小值3,由
上有最小值3,由 ,
,
① 當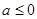 時,
時, ,
, 在
在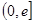 上單調遞減,
上單調遞減,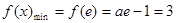 ,解得
,解得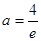 ,舍去. 8分
,舍去. 8分
②當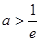 即
即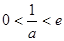 時,
時, 在
在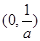 上單調遞減,在
上單調遞減,在 上單調遞增,
上單調遞增,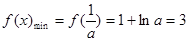 ,解得
,解得 ,滿足條件. 10分
,滿足條件. 10分
③ 當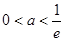 即
即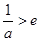 時,
時, ,
,
所以 在
在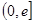 上單調遞減,
上單調遞減,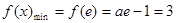 ,解得
,解得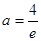 ,舍去.
,舍去.
綜上,存在實數 ,使
,使 在區間
在區間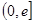 上的最小值是3. 12分
上的最小值是3. 12分
考點:導數的幾何意義 導數的應用 分類討論思想


 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com