
已知各項均為正數的數列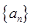 的前
的前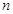 項和為
項和為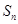 ,數列
,數列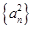 的前
的前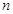 項和為
項和為 ,且
,且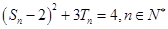 .
.
⑴證明:數列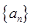 是等比數列,并寫出通項公式;
是等比數列,并寫出通項公式;
⑵若 對
對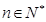 恒成立,求
恒成立,求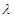 的最小值;
的最小值;
⑶若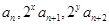 成等差數列,求正整數
成等差數列,求正整數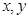 的值.
的值.
(1)證明見解析, ;(2)3;(3)
;(2)3;(3)
解析試題分析:(1)要證數列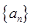 是等比數列,可根據題設求出
是等比數列,可根據題設求出 ,當然也可再求
,當然也可再求 ,雖然得出的
,雖然得出的 成等比數列,但前面有限項成等比不能說明所有項都成等比,必須嚴格證明.一般方法是把已知式
成等比數列,但前面有限項成等比不能說明所有項都成等比,必須嚴格證明.一般方法是把已知式 中的
中的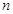 用
用 代換得到
代換得到 ,兩式相減得
,兩式相減得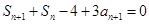 ,這個式子中把
,這個式子中把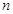 用
用 代換又得
代換又得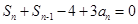 ,兩式再相減,正好得出數列的前后項關系的遞推關系
,兩式再相減,正好得出數列的前后項關系的遞推關系 ,正是等比數列的表現.(2)由題間
,正是等比數列的表現.(2)由題間 ,對不等式
,對不等式 用分離參數法得
用分離參數法得 ,求
,求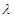 的最小值就與求
的最小值就與求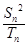 的最大值(也只要能是取值范圍)聯系起來了.(3)只能由
的最大值(也只要能是取值范圍)聯系起來了.(3)只能由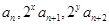 成等差數列列出唯一的等式,這個等式是關于
成等差數列列出唯一的等式,這個等式是關于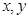 的二元方程,它屬于不定方程,有無數解,只是由于
的二元方程,它屬于不定方程,有無數解,只是由于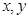 都是正整數,利用正整數的性質可得出具體的解.
都是正整數,利用正整數的性質可得出具體的解.
試題解析:(1)當n=1時, ;當n=2時,
;當n=2時,
當n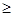 3時,有
3時,有 得:
得:
化簡得: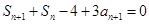 3分
3分
又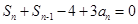 ∴
∴
∴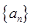 是1為首項,
是1為首項,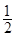 為公比的等比數列
為公比的等比數列 6分
6分
(2)
∴ ∴
∴ 11分
11分
(3)若三項成等差,則有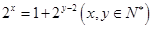
 ,右邊為大于2的奇數,左邊為偶數或1,不成立
,右邊為大于2的奇數,左邊為偶數或1,不成立
∴ 16分
16分
考點:(1)等比數列的通項公式;(2)不等式恒成立與函數的最值;(3)不定方程的正整數解問題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
已知數列{an}是等差數列,a2=6,a5=12,數列{bn}的前n項和是Sn,且Sn+ bn=1.
bn=1.
(1)求數列{an}的通項公式.
(2)求證:數列{bn}是等比數列.
(3)記cn=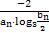 ,{cn}的前n項和為Tn,若Tn<
,{cn}的前n項和為Tn,若Tn<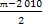 對一切n∈N*都成立,求最小正整數m.
對一切n∈N*都成立,求最小正整數m.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知等比數列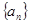 的公比為
的公比為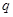 ,
,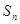 是
是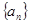 的前
的前 項和.
項和.
(1)若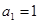 ,
,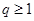 ,求
,求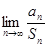 的值;
的值;
(2)若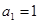 ,
,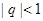 ,
,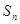 有無最值?并說明理由;
有無最值?并說明理由;
(3)設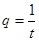 ,若首項
,若首項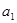 和
和 都是正整數,
都是正整數, 滿足不等式:
滿足不等式: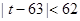 ,且對于任意正整數
,且對于任意正整數 有
有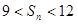 成立,問:這樣的數列
成立,問:這樣的數列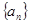 有幾個?
有幾個?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,設曲線
,設曲線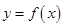 在點
在點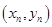 處的切線與
處的切線與 軸的交點為
軸的交點為 ,其中
,其中 為正實數.
為正實數.
(1)用 表示
表示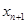 ;
;
(2)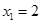 ,若
,若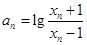 ,試證明數列
,試證明數列 為等比數列,并求數列
為等比數列,并求數列 的通項公式;
的通項公式;
(3)若數列 的前
的前 項和
項和 ,記數列
,記數列 的前
的前 項和
項和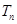 ,求
,求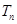 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
大學生自主創業已成為當代潮流.某大學大三學生夏某今年一月初向銀行貸款兩萬元作開店資金,全部用作批發某種商品.銀行貸款的年利率為6%,約定一年后一次還清貸款.已知夏某每月月底獲得的利潤是該月月初投人資金的15%,每月月底需要交納個人所得稅為該月所獲利潤的20%,當月房租等其他開支1500元,余款作為資金全部投入批發該商品再經營,如此繼續,假定每月月底該商品能全部賣出.
(1)設夏某第n個月月底余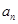 元,第n+l個月月底余
元,第n+l個月月底余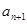 元,寫出a1的值并建立
元,寫出a1的值并建立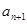 與
與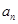 的遞推關系;
的遞推關系;
(2)預計年底夏某還清銀行貸款后的純收入.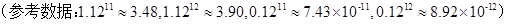
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知等比數列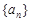 滿足
滿足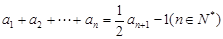 .
.
(1)求數列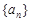 的通項公式;
的通項公式;
(2)在 與
與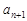 之間插入
之間插入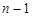 個數連同
個數連同 與
與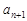 按原順序組成一個公差為
按原順序組成一個公差為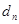 (
(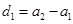 )的等差數列.
)的等差數列.
①設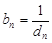 ,求數列
,求數列 的前
的前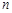 和
和 ;
;
②在數列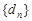 中是否存在三項
中是否存在三項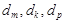 (其中
(其中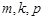 成等差數列)成等比數列?若存在,求出這樣的三項;若不存在,說明理由.
成等差數列)成等比數列?若存在,求出這樣的三項;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
給定數列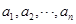 .對
.對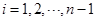 ,該數列前
,該數列前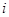 項的最大值記為
項的最大值記為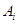 ,后
,后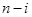 項
項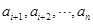 的最小值記為
的最小值記為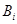 ,
,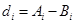 .
.
(Ⅰ)設數列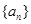 為
為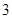 ,
, ,
,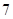 ,
, ,寫出
,寫出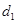 ,
,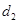 ,
, 的值;
的值;
(Ⅱ)設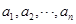
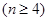 是公比大于
是公比大于 的等比數列,且
的等比數列,且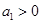 .證明:
.證明: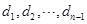 是等比數列.
是等比數列.
(Ⅲ)設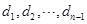 是公差大于
是公差大于 的等差數列,且
的等差數列,且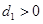 ,證明:
,證明: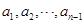 是等差數列.
是等差數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com