Question

素材1：直線l₁:12x+6y-72=0.

素材2：直線l₂:ax+y-2=0.

先將上面的素材構建成一個問題，然后再解答.

Answer 1

構建問題：直線l₁:12x+6y-72=0,直線l₂:ax+y-2=0.

若上述兩直線l₁、l₂與x、y軸的正半軸圍成的四邊形有外接圓，求外接圓的方程.

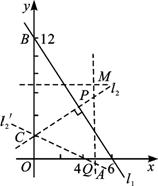
解析：設直線l₁與x、y軸的交點分別為A（6，0）、B（0，12），直線l₂與y軸的交點為C（0，2）.

（1）當l₁⊥l₂時，設垂足為P，又OA⊥OC.

∴四點O、A、P、C共圓且以AC為直徑.

∴所求方程為x(x-6)+y(y-2)=0，即x²+y²-6x-2y=0.

（2)當l₁與l₂不垂直時，設l₂與x軸的正半軸交于點Q，若A、B、C、Q四點共圓，

則|OQ|·|OA|=|OC|·|OB|，

∴|OQ|=4.∴圓心M在線段BC、QA的中垂線上.∴M(5，7).

又|MA|=，

∴所求圓的方程為（x-5）²+(y-7)²=50.