
已知函數(shù)f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且關于x的方程f(x)=m有兩個不同的正數(shù)解,求實數(shù)m的取值范圍;
(2)設函數(shù)g(x)=" f(" x),x∈[ 2,+∞), 滿足如下性質:若存在最大(小)值,則最大(小)值與a無關.試求a的取值范圍.
滿足如下性質:若存在最大(小)值,則最大(小)值與a無關.試求a的取值范圍.
(1)實數(shù) 的取值范圍為區(qū)間
的取值范圍為區(qū)間 ;(2)實數(shù)a的取值范圍是
;(2)實數(shù)a的取值范圍是 .
.
解析試題分析:(1)令 ,換元將問題轉化為關于
,換元將問題轉化為關于 的方程
的方程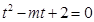 有相異的且均大于1的兩根,利用二次函數(shù)的性質解答即可;(2)算得
有相異的且均大于1的兩根,利用二次函數(shù)的性質解答即可;(2)算得 ,分類討論①當
,分類討論①當 ,②當
,②當 ,再分
,再分 ,
, 討論解答.
討論解答.
試題解析:(1)令 ,
, ,因為
,因為 ,所以
,所以 ,所以關于
,所以關于 的方程
的方程 有兩個不同的正數(shù)解等價于關于
有兩個不同的正數(shù)解等價于關于 的方程
的方程 有相異的且均大于1的兩根,即關于
有相異的且均大于1的兩根,即關于 的方程
的方程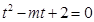 有相異的且均大于1的兩根, 2分
有相異的且均大于1的兩根, 2分
所以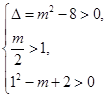 , 4分
, 4分
解得 ,故實數(shù)
,故實數(shù) 的取值范圍為區(qū)間
的取值范圍為區(qū)間 . 6分
. 6分
(2)
①當 時,
時,
a) 時,
時, ,
, ,所以
,所以  ,
,
b) 時,
時,
 ,所以
,所以  8分
8分
ⅰ)當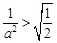 即
即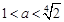 時,對
時,對 ,
, ,所以
,所以  在
在 上遞增,
上遞增,
所以  ,綜合a) b)
,綜合a) b) 有最小值為
有最小值為 與a有關,不符合 10分
與a有關,不符合 10分
ⅱ)當 即
即 時,由
時,由 得
得 ,且當
,且當 時,
時, ,當
,當 時,
時, ,所以
,所以  在
在 上遞減,在
上遞減,在 上遞增,所以
上遞增,所以
 ,綜合a) b)
,綜合a) b)  有最小值為
有最小值為 與a無關,符合要求. 12分
與a無關,符合要求. 12分
②當 時,
時,
a)  時,
時, ,
, ,所以
,所以 
b)  時,
時, ,
, ,
,
所以 
 ,
, 在
在 上遞減,
上遞減,
所以  ,綜合a) b)
,綜合a) b)  有最大值為
有最大值為 與a有關,不符合 15分
與a有關,不符合 15分
綜上所述,實數(shù)a的取值范圍是 . &
. &


科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) =
= ,
, =
= ,若曲線
,若曲線 和曲線
和曲線 都過點P(0,2),且在點P處有相同的切線
都過點P(0,2),且在點P處有相同的切線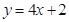 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若 時,
時, ≤
≤ ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
新晨投資公司擬投資開發(fā)某項新產品,市場評估能獲得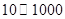 萬元的投資收益.現(xiàn)公司準備制定一個對科研課題組的獎勵方案:獎金
萬元的投資收益.現(xiàn)公司準備制定一個對科研課題組的獎勵方案:獎金 (單位:萬元)隨投資收益
(單位:萬元)隨投資收益 (單位:萬元)的增加而增加,且獎金不低于
(單位:萬元)的增加而增加,且獎金不低于 萬元,同時不超過投資收益的
萬元,同時不超過投資收益的 .
.
(1)設獎勵方案的函數(shù)模型為 ,試用數(shù)學語言表述公司對獎勵方案的函數(shù)模型
,試用數(shù)學語言表述公司對獎勵方案的函數(shù)模型 的基本要求.
的基本要求.
(2)下面是公司預設的兩個獎勵方案的函數(shù)模型:
① ; ②
; ②
試分別分析這兩個函數(shù)模型是否符合公司要求.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,某生態(tài)園欲把一塊四邊形地 辟為水果園,其中
辟為水果園,其中 ,
, 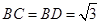 ,
, .若經(jīng)過
.若經(jīng)過 上一點
上一點 和
和 上一點
上一點 鋪設一條道路
鋪設一條道路 ,且
,且 將四邊形
將四邊形 分成面積相等的兩部分,設
分成面積相等的兩部分,設 .
.
(1)求 的關系式;
的關系式;
(2)如果 是灌溉水管的位置,為了省錢,希望它最短,求
是灌溉水管的位置,為了省錢,希望它最短,求 的長的最小值;
的長的最小值;
(3)如果 是參觀路線,希望它最長,那么
是參觀路線,希望它最長,那么 的位置在哪里?
的位置在哪里?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
統(tǒng)計表明:某種型號的汽車在勻速行駛中每小時的耗油量 (升)關于行駛速度
(升)關于行駛速度 (千米/每小時)的函數(shù)解析式可以表示為
(千米/每小時)的函數(shù)解析式可以表示為 ,已知甲、乙兩地相距100千米.
,已知甲、乙兩地相距100千米.
(1)當汽車以40千米/小時的速度行駛時,從甲地到乙地要耗油多少升?
(2)當汽車以多大速度行駛時,從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com