
已知函數(shù)f(x)=4cos ωx· (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(1)求ω的值;
(2)討論f(x)在區(qū)間 上的單調(diào)性.
上的單調(diào)性.
(1)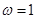 (2)
(2) 在
在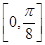 單調(diào)遞增,在
單調(diào)遞增,在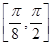 單調(diào)遞減.
單調(diào)遞減.
解析試題分析:(1)利用兩角和正弦公式和降冪公式化簡,得到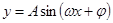 的形式,利用公式
的形式,利用公式 計算周期.(2)利用正弦函數(shù)的單調(diào)區(qū)間,求在
計算周期.(2)利用正弦函數(shù)的單調(diào)區(qū)間,求在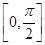 的單調(diào)性.(3)求三角函數(shù)的最小正周期一般化成
的單調(diào)性.(3)求三角函數(shù)的最小正周期一般化成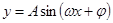 ,
, ,
, 形式,利用周期公式即可.(4)求解較復(fù)雜三角函數(shù)的單調(diào)區(qū)間時,首先化成
形式,利用周期公式即可.(4)求解較復(fù)雜三角函數(shù)的單調(diào)區(qū)間時,首先化成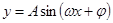 形式,再
形式,再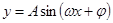 的單調(diào)區(qū)間,只需把
的單調(diào)區(qū)間,只需把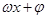 看作一個整體代入
看作一個整體代入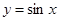 相應(yīng)的單調(diào)區(qū)間,注意先把
相應(yīng)的單調(diào)區(qū)間,注意先把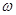 化為正數(shù),這是容易出錯的地方.
化為正數(shù),這是容易出錯的地方.
試題解析:解:(1)f(x)=4cos ωx·sin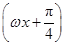
=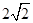 sin ωx·cos ωx+
sin ωx·cos ωx+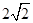 cos2ωx
cos2ωx
=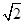 (sin 2ωx+cos 2ωx)+
(sin 2ωx+cos 2ωx)+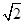
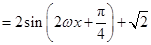 3分
3分
因為f(x)的最小正周期為π,且ω>0,
從而有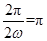 ,故ω=1. 6分
,故ω=1. 6分
(2)由(1)知,f(x)=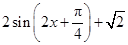 .
.
若0≤x≤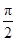 ,則
,則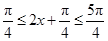 .
.
當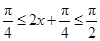 ,即
,即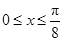 時,f(x)單調(diào)遞增;
時,f(x)單調(diào)遞增;
當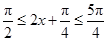 ,即
,即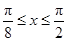 時,f(x)單調(diào)遞減. 10分
時,f(x)單調(diào)遞減. 10分
綜上可知,f(x)在區(qū)間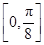 上單調(diào)遞增,在區(qū)間
上單調(diào)遞增,在區(qū)間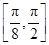 上單調(diào)遞減. 12分
上單調(diào)遞減. 12分
考點:(1)利用公式對三角函數(shù)進行化簡.(2)求正弦型函數(shù)的單調(diào)區(qū)間.


 閱讀快車系列答案
閱讀快車系列答案國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com