
(在數學趣味知識培訓活動中,甲、乙兩名學生的6次培訓成績如下莖葉圖所示: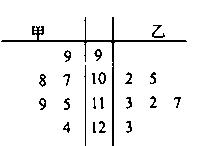
(Ⅰ)從甲、乙兩人中選擇1人參加數學趣味知識競賽,你會選哪位?請運用統計學的知識說明理由;
(II)從乙的6次培訓成績中隨機選擇2個,記被抽到的分數超過115分的個數為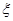 ,試求
,試求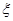 的分布列和數學期望.
的分布列和數學期望.
(I)選擇乙;(II)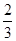 .
.
解析試題分析:(I)根據莖葉圖,寫出兩個同學的成績,對于這兩個同學的成績求出平均數,結果兩人的平均數相等,再比較兩個人的方差,得到乙的方差較小,這樣可以派乙去,因為乙的成績比較穩定.(II)由題意知本題是一個古典概型,試驗發生包含的所有事件是從乙的6次培訓成績中隨機選擇2個,滿足事件的恰好有2次,記被抽到的分數超過115分的個數為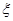 ,由題意值
,由題意值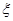 可取0,1,2,根據古典概型的概率公式求出對應的概率,寫出分布列,求出期望.
可取0,1,2,根據古典概型的概率公式求出對應的概率,寫出分布列,求出期望.
試題解析:(I)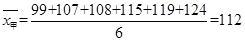 ;
;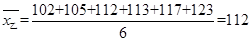 .
.
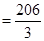
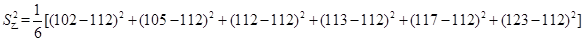
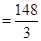
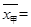
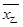 ;
;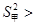
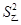 .
.
所以,甲乙兩方的平均水平一樣,乙的方差小,乙發揮的更穩定,則選擇乙.
(II)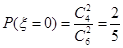 ;
; 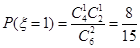 ;
;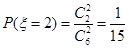 .
.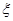 的分布列為:
的分布列為:
所以數學期望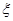
0 1 2 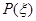
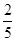
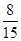
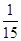
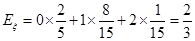 .
.
考點:1.莖葉圖;2.平均數與方差;3.離散型隨機變量及其分布列;4.期望.


科目:高中數學 來源: 題型:解答題
城市公交車的數量若太多則容易造成資源的浪費;若太少又難以滿足乘客需求.某市公交公司在某站臺的60名候車乘客中隨機抽取15人,將他們的候車時間作為樣本分成5組,如下表所示(單位:分鐘):
| 組別 | 候車時間 | 人數 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某次有1000人參加的數學摸底考試,其成績的頻率分布直方圖如圖所示,規定85分及其以上為優秀.
(1)下表是這次考試成績的頻數分布表,求正整數a, b的值;
| 區間 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人數 | 50 | a | 350 | 300 | b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在每年的春節后,某市政府都會發動公務員參與到植樹活動中去.為保證樹苗的質量,該市林管部門在植樹前,都會在植樹前對樹苗進行檢測.現從甲乙兩種樹苗中各抽測了10株樹苗的高度,量出樹苗的高度如下(單位:厘米):
甲:
乙:
(1)根據抽測結果,完成答題卷中的莖葉圖,并根據你填寫的莖葉圖,對甲、乙兩種樹苗的高度作比較,寫出兩個統計結論;
(2)設抽測的10株甲種樹苗高度平均值為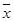 ,將這10株樹苗的高度依次輸入按程序框圖進行的運算,問輸出的
,將這10株樹苗的高度依次輸入按程序框圖進行的運算,問輸出的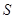 大小為多少?并說明
大小為多少?并說明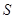 的統計學意義.
的統計學意義.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在“2013魅力新邢臺”青少年才藝表演評比活動中,參賽選手成績的莖葉圖和頻率分布直方圖,都受到不同程度的損壞,回答問題

(1)求參賽總人數和頻率分布直方圖中 之間的矩形的高,并完成直方圖;
之間的矩形的高,并完成直方圖;
(2)若要從分數在 之間任取兩份進行分析,在抽取的結果中,求至少有一份分數在
之間任取兩份進行分析,在抽取的結果中,求至少有一份分數在 之間的概率.
之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某同學在生物研究性學習中,對春季晝夜溫差大小與黃豆種子發芽多少之間的關系進行研究,于是他在4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每100顆種子浸泡后的發芽數,得到如下資料:
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發芽數 顆 顆 | 23 | 25 | 30 | 26 | 16 |
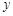 關于
關于 的線性回歸方程
的線性回歸方程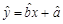 ;
;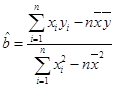
 ,
, )
)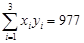 ,
, )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學高三年級從甲、乙兩個班級各選出七名學生參加數學競賽,他們取得的成績(滿分100分)的莖葉圖如圖所示,其中甲班學生的平均分是85,乙班學生成績的中位數是83,
(1)求x和y的值;
(2)計算甲班七名學生成績的方差;
(3)從成績在90分以上的學生中隨機抽取兩名學生,求甲班至少有一名學生的概率.
參考公式:方差 其中
其中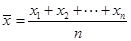
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
學校為了預防甲流感,每天上午都要對同學進行體溫抽查。某一天,隨機抽取甲、乙兩個班級各10名同學,測量他們的體溫如圖:(單位0.1℃)
(1)哪個班所選取的這10名同學的平均體溫高?
(2)一般 ℃為低熱,
℃為低熱, ℃為中等熱,
℃為中等熱, ℃為高熱。按此規定,記事件A為“從甲班發熱的同學中任選兩人,有中等熱的同學”,記事件B為“從乙班發熱的同學中任選兩人,有中等熱的同學”,分別求事件A和事件B的概率.
℃為高熱。按此規定,記事件A為“從甲班發熱的同學中任選兩人,有中等熱的同學”,記事件B為“從乙班發熱的同學中任選兩人,有中等熱的同學”,分別求事件A和事件B的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知某池塘養殖著鯉魚和鯽魚,為了估計這兩種魚的數量,養殖者從池塘中捕出兩種魚各 只,給每只魚做上不影響其存活的標記,然后放回池塘,待完全混合后,再每次從池塘中隨機的捕出
只,給每只魚做上不影響其存活的標記,然后放回池塘,待完全混合后,再每次從池塘中隨機的捕出 只魚,記錄下其中有記號的魚的數目,立即放回池塘中。這樣的記錄做了
只魚,記錄下其中有記號的魚的數目,立即放回池塘中。這樣的記錄做了 次,并將記錄獲取的數據做成以下的莖葉圖。
次,并將記錄獲取的數據做成以下的莖葉圖。
(Ⅰ)根據莖葉圖計算有記號的鯉魚和鯽魚數目的平均數,并估計池塘中的鯉魚和鯽魚的數量;
(Ⅱ)為了估計池塘中魚的總重量,現從中按照(Ⅰ)的比例對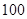 條魚進行稱重,據稱重魚的重量介于
條魚進行稱重,據稱重魚的重量介于 (單位:千克)之間,將測量結果按如下方式分成九組:第一組
(單位:千克)之間,將測量結果按如下方式分成九組:第一組 、第二組
、第二組 ;……,第九組
;……,第九組 。右圖是按上述分組方法得到的頻率分布直方圖的一部分。
。右圖是按上述分組方法得到的頻率分布直方圖的一部分。
①估計池塘中魚的重量在 千克以上(含
千克以上(含 千克)的條數;
千克)的條數;
②若第二組、第三組、第四組魚的條數依次成公差為 的等差數列,請將頻率分布直方圖補充完整;
的等差數列,請將頻率分布直方圖補充完整;
③在②的條件下估計池塘中魚的重量的眾數、中位數及估計池塘中魚的總重量;
(Ⅲ)假設隨機地從池塘逐只有放回的捕出 只魚中出現鯉魚的次數為
只魚中出現鯉魚的次數為 ,求
,求 的數學期望。
的數學期望。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com