
定義在R上的單調函數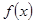 滿足
滿足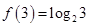 且對任意
且對任意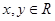 都有
都有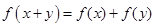 .
.
(1)求證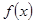 為奇函數;
為奇函數;
(2)若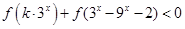 對任意
對任意 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(1)證明:利用“賦值法”,確定f(0)=0,再
計算f(x)+f(-x)=0.
(2) t=3 >0,換元后,問題等價于t
>0,換元后,問題等價于t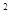 -(1+k)t+2>0
-(1+k)t+2>0
假設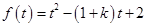 ,當
,當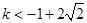 時,
時,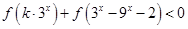 對任意
對任意 恒成立.
恒成立.
解析試題分析:
思路分析:(1)證明:利用“賦值法”,確定f(0)=0,再
計算f(x)+f(-x)=0.
(2) t=3 >0,換元后,問題等價于t
>0,換元后,問題等價于t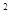 -(1+k)t+2>0
-(1+k)t+2>0
假設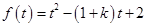 ,應用二次函數的圖象和性質進一步求解。
,應用二次函數的圖象和性質進一步求解。
(1)證明:f(x+y)=f(x)+f(y) (x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
則有0=f(x)+f(-x).即f(-x)=-f(x)對任意x∈R成立,
所以f(x)是奇函數.
(2)解: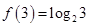 >0,即f(3)>f(0),又
>0,即f(3)>f(0),又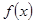 在R上是單調函數,
在R上是單調函數,
所以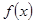 在R上是增函數
在R上是增函數
又由(1)f(x)是奇函數.f(k·3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2),
+2),
∴ k·3 <-3
<-3 +9
+9 +2,3
+2,3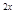 -(1+k)·3
-(1+k)·3 +2>0對任意x∈R成立.
+2>0對任意x∈R成立.
令t=3 >0,問題等價于t
>0,問題等價于t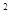 -(1+k)t+2>0
-(1+k)t+2>0
對任意t>0恒成立.
令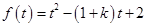 ,其對稱軸
,其對稱軸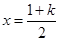
當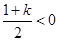 即
即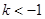 時,
時,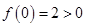 符合題意;
符合題意;
當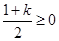 時,對任意
時,對任意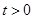 ,
,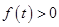 恒成立
恒成立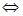
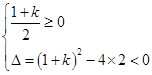
解得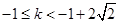
綜上所述,當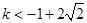 時,
時,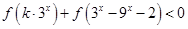 對任意
對任意 恒成立.
恒成立.
考點:函數的單調性,指數函數的性質,二次函數的圖象和性質。
點評:中檔題,本題涉及抽象函數問題,一般要考慮應用“賦值法”,確定所需數據。本題通過換元,將問題轉化成二次函數的圖象和性質應用問題,具有“化生為熟”的示范作用。


科目:高中數學 來源: 題型:解答題
已知函數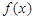 的定義域為
的定義域為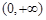 ,若
,若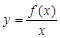 在
在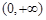 上為增函數,則稱
上為增函數,則稱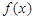 為“一階比增函數”;若
為“一階比增函數”;若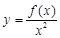 在
在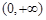 上為增函數,則稱
上為增函數,則稱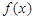 為“二階比增函數”.我們把所有“一階比增函數”組成的集合記為
為“二階比增函數”.我們把所有“一階比增函數”組成的集合記為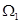 ,所有“二階比增函數”組成的集合記為
,所有“二階比增函數”組成的集合記為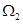 .
.
(Ⅰ)已知函數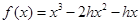 ,若
,若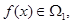 且
且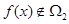 ,求實數
,求實數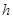 的取值范圍;
的取值范圍;
(Ⅱ)已知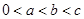 ,
,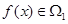 且
且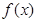 的部分函數值由下表給出,
的部分函數值由下表給出,
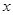 |  | 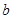 | 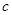 |  |
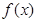 | 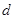 | 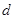 | 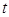 | 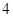 |
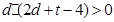 ;
;
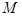 ,使得
,使得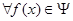 ,
,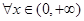 ,有
,有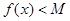 成立?若存在,求出
成立?若存在,求出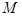 的最小值;若不存在,說明理由.
的最小值;若不存在,說明理由.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位設計的兩種密封玻璃窗如圖所示:圖1是單層玻璃,厚度為8 mm;圖2是雙層中空玻璃,厚度均為4 mm,中間留有厚度為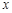 的空氣隔層.根據熱傳導知識,對于厚度為
的空氣隔層.根據熱傳導知識,對于厚度為 的均勻介質,兩側的溫度差為
的均勻介質,兩側的溫度差為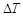 ,單位時間內,在單位面積上通過的熱量
,單位時間內,在單位面積上通過的熱量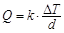 ,其中
,其中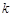 為熱傳導系數.假定單位時間內,在單位面積上通過每一層玻璃及空氣隔層的熱量相等.(注:玻璃的熱傳導系數為
為熱傳導系數.假定單位時間內,在單位面積上通過每一層玻璃及空氣隔層的熱量相等.(注:玻璃的熱傳導系數為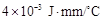 ,空氣的熱傳導系數為
,空氣的熱傳導系數為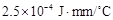 .)
.)
(1)設室內,室外溫度均分別為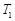 ,
,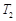 ,內層玻璃外側溫度為
,內層玻璃外側溫度為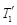 ,外層玻璃內側溫度為
,外層玻璃內側溫度為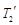 ,且
,且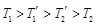 .試分別求出單層玻璃和雙層中空玻璃單位時間內,在單位面積上通過的熱量(結果用
.試分別求出單層玻璃和雙層中空玻璃單位時間內,在單位面積上通過的熱量(結果用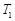 ,
,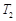 及
及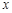 表示);
表示);
(2)為使雙層中空玻璃單位時間內,在單位面積上通過的熱量只有單層玻璃的4%,應如何設計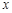 的大小?
的大小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(14分)已知函數 ,其中a是實數.設A(x1,f(x1)),B(x2,f(x2))為該函數圖象上的兩點,且x1<x2.
,其中a是實數.設A(x1,f(x1)),B(x2,f(x2))為該函數圖象上的兩點,且x1<x2.
(Ⅰ)指出函數f(x)的單調區間;
(Ⅱ)若函數f(x)的圖象在點A,B處的切線互相垂直,且x2<0,證明:x2﹣x1≥1;
(Ⅲ)若函數f(x)的圖象在點A,B處的切線重合,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲廠以x 千克/小時的速度運輸生產某種產品(生產條件要求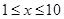 ),每小時可獲得利潤是
),每小時可獲得利潤是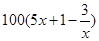 元.
元.
(1)要使生產該產品2小時獲得的利潤不低于3000元,求x的取值范圍;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com