
(本題滿分為12分)
已知函數 的圖像過坐標原點
的圖像過坐標原點 ,且在點
,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(1)求實數 的值;
的值;
(2)求 在區間
在區間 上的最大值;
上的最大值;
(3)對任意給定的正實數 ,曲線
,曲線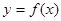 上是否存在兩點
上是否存在兩點 ,使得
,使得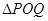 是以
是以 為直角頂點的直角三角形,且此三角形斜邊的中點在軸上?請說明理由.
為直角頂點的直角三角形,且此三角形斜邊的中點在軸上?請說明理由.
(1)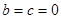 (2)當
(2)當 ,即
,即 時,
時,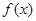 在
在 上的最大值為2;當
上的最大值為2;當 ,即
,即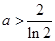 時,
時,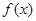 在
在 上的最大值為
上的最大值為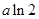 .(3)存在。
.(3)存在。
【解析】
試題分析:解:
(I)當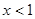 時,
時, 則
則 . (1分)
. (1分)
依題意,得 即
即 ,解得
,解得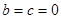 . (3分)
. (3分)
(II)由(1)知,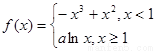
①當 時
時
令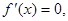 得
得 或
或 (4分)
(4分)
當 變化時
變化時 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
( |
|
|
- |
|
|
|
- |
|
|
單調遞減 |
極小值 |
單調遞增 |
極大值 |
單調遞減 |
又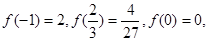
所以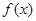 在
在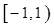 上的最大值為
上的最大值為 . (6分)
. (6分)
②當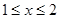 時,
時,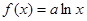
當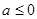 時,
時,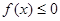 ,所以
,所以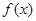 的最大值為0 ;
的最大值為0 ;
當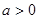 時,
時,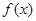 在
在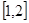 上單調遞增,所以
上單調遞增,所以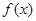 在
在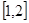 上的最大值為
上的最大值為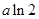 .(7分)
.(7分)
綜上所述,
當 ,即
,即 時,
時,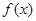 在
在 上的最大值為2;
上的最大值為2;
當 ,即
,即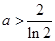 時,
時,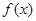 在
在 上的最大值為
上的最大值為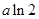 . (8分)
. (8分)
(III)假設曲線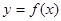 上存在兩點
上存在兩點 滿足題設要求,則點
滿足題設要求,則點 只能在y軸的兩側.
只能在y軸的兩側.
不妨設 ,則
,則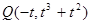 ,顯然
,顯然
因為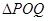 是以
是以 為直角頂點的直角三角形,
為直角頂點的直角三角形,
所以 ,即
,即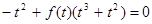 ①
①
若方程①有解,則存在滿足題意的兩點 ;若方程①無解,則不存在滿足題意的兩點
;若方程①無解,則不存在滿足題意的兩點
若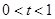 ,則
,則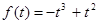 ,代入①式得
,代入①式得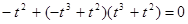 ,
,
即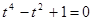 ,而此方程無實數解,因此
,而此方程無實數解,因此 . (10分)
. (10分)
此時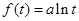 ,代入①式得,
,代入①式得,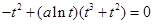 即
即 ②
②
令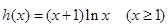 ,則
,則 ,所以
,所以 在
在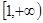 上單調遞增,
上單調遞增,
因為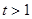 ,所以
,所以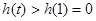 ,當
,當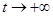 時,
時,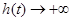 ,所以
,所以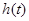 的取值范圍為
的取值范圍為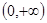 .所以對于
.所以對于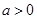 ,方程②總有解,即方程①總有解.
,方程②總有解,即方程①總有解.
因此對任意給定的正實數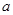 ,曲線
,曲線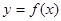 上總存在兩點
上總存在兩點 ,使得
,使得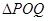 是以
是以 為直角頂點的直角三角形,且此三角形斜邊的中點在y軸上. (12分)
為直角頂點的直角三角形,且此三角形斜邊的中點在y軸上. (12分)
考點:導數的運算;函數的最值與導數的關系。
點評:在新課標中,導數是重要的知識點,由于它對求函數的單調性、最值由很大的幫助,因而成為考試的熱點。


科目:高中數學 來源:2015屆遼寧省錦州市高一12月月考數學試卷(解析版) 題型:解答題
(本題滿分為12分)
如圖所示:已知 ⊙O所在的平面,AB是⊙O的直徑,C是⊙O上任意一點,過A作
⊙O所在的平面,AB是⊙O的直徑,C是⊙O上任意一點,過A作 于E,求證:
于E,求證: .
.

查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧沈陽二中等重點中學協作體高三領航高考預測十二理數學卷(解析版) 題型:解答題
(本題滿分為12分)
已知橢圓中心在原點,焦點在y軸上,焦距為4,離心率為 .
.
(I)求橢圓方程;
(II)設橢圓在y軸的正半軸上的焦點為M,又點A和點B在橢圓上,且M分有向線段 所成的比為2,求線段AB所在直線的方程.
所成的比為2,求線段AB所在直線的方程.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三上學期第一次檢測理科數學試卷(解析版) 題型:解答題
(本題滿分為12分)
已知函數 的圖像過坐標原點
的圖像過坐標原點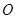 ,且在點
,且在點 處的切線
處的切線
的斜率是 .
.
(1)求實數 的值; (2)求
的值; (2)求 在區間
在區間 上的最大值;
上的最大值;
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三上學期第一次檢測理科數學試卷(解析版) 題型:解答題
(本題滿分為12分)已知橢圓中心在原點,焦點在y軸上,焦距為4,離心率為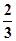 .
.

(I)求橢圓方程;
(II)設橢圓在y軸的正半軸上的焦點為M,又點A和點B在橢圓上,且M分有向線段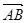 所成的比為2,求線段AB所在直線的方程.
所成的比為2,求線段AB所在直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com