
已知點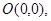
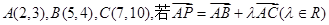
(1)是否存在 ,使得點P在第一、三象限的角平分線上?
,使得點P在第一、三象限的角平分線上?
(2)是否存在 ,使得四邊形
,使得四邊形 為平行四邊形?(若存在,則求出
為平行四邊形?(若存在,則求出 的值,若不存在,請說明理由.)
的值,若不存在,請說明理由.)
(1)存在;(2)不存在.
解析試題分析:(1)根據已知的等式求得P的坐標,再根據P在第一、三象限角平分線上可以得到P的坐標滿足 ,從而可以建立關于
,從而可以建立關于 的方程,方程組的解的情況即是
的方程,方程組的解的情況即是 的存在情況;(2)由四邊形OBPA是平行四邊形,結合向量加法的平行四邊形法則,可以得到
的存在情況;(2)由四邊形OBPA是平行四邊形,結合向量加法的平行四邊形法則,可以得到 ,從而建立關于
,從而建立關于 的方程組,方程組的解的情況即是
的方程組,方程組的解的情況即是 的存在情況.
的存在情況.
(1)存在.
設 ,則
,則 ,∵
,∵ 3分
3分
由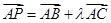 得
得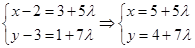 5分
5分
若點P在第一、三象限的角平分線上,則 ,即
,即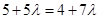 ,
, . 6分
. 6分
(2)不存在.
若四邊形OBPA為平行四邊形,則 8分
8分
∵ ,∴
,∴ ,方程組無解,因此滿足條件的
,方程組無解,因此滿足條件的 不存在 10分
不存在 10分
考點:1、向量的坐標運算;2、第一、三象限角平分線上點的坐標特點3、向量加法的平行四邊形法則.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源: 題型:解答題
已知向量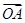 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).
=(5-m,-3-m).
(1)若點A,B,C不能構成三角形,求實數m滿足的條件;
(2)若△ABC為直角三角形,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設a、b是不共線的兩個非零向量,
(1)若 =2a-b,
=2a-b, =3a+b,
=3a+b,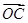 =a-3b,求證:A、B、C三點共線;
=a-3b,求證:A、B、C三點共線;
(2)若8a+kb與ka+2b共線,求實數k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知平面向量a=( ,-1),b=
,-1),b=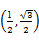 .
.
(1)若x=(t+2)a+(t2-t-5)b,y=-ka+4b(t,k∈R),且x⊥y,求出k關于t的關系式k=f(t).
(2)求函數k=f(t)在t∈(-2,2)上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知復平面內平行四邊形ABCD(A,B,C,D按逆時針排列),A點對應的復數為2+i,向量 對應的復數為1+2i,向量
對應的復數為1+2i,向量 對應的復數為3-i.
對應的復數為3-i.
(1)求點C,D對應的復數.
(2)求平行四邊形ABCD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 ,點B是
,點B是 軸上的動點,過B作AB的垂線
軸上的動點,過B作AB的垂線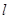 交
交 軸于點Q,若
軸于點Q,若 ,
, .
.
(1)求點P的軌跡方程;
(2)是否存在定直線 ,以PM為直徑的圓與直線
,以PM為直徑的圓與直線 的相交弦長為定值,若存在,求出定直線方程;若不存在,請說明理由。
的相交弦長為定值,若存在,求出定直線方程;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com