
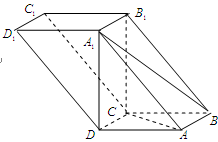
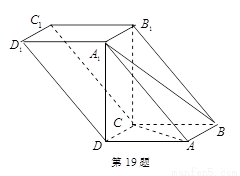
如圖,四棱柱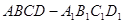 中,
中,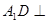 平面
平面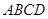 ,底面
,底面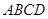 是邊長為1的正方形,側棱
是邊長為1的正方形,側棱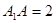 ,
,

(Ⅰ)證明: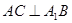 ;
;
(Ⅱ)若棱 上存在一點
上存在一點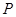 ,使得
,使得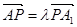 ,
,
當二面角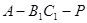 的大小為
的大小為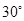 時,求實數
時,求實數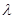 的值.
的值.
以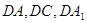 所在直線分別為
所在直線分別為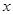 軸,
軸,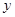 軸,
軸, 軸建系
軸建系
(Ⅱ) .
.
【解析】
試題分析:(I)(Ⅰ)連接BD交AC于點O
∵四邊形ABCD是正方形∴AC⊥BD
又∵AD1⊥平面ABCD,AC?平面ABCD
∴AC⊥A1D,A1D∩BD=D∴AC⊥平面A1BD,A1B?平面A1BD
∴AC⊥A1B。
以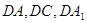 所在直線分別為
所在直線分別為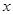 軸,
軸,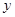 軸,
軸, 軸建系
軸建系
(Ⅱ)∵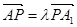 ∴
∴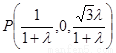 ,設平面
,設平面 的一個法向量為
的一個法向量為 ,
,
 ,
,
令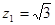 則
則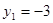 ,
, ,
,
∴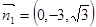 6分
6分
設平面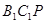 的一個法向量為
的一個法向量為
 ,
,

∴ 8分
8分
 10分
10分
∴ 12分
12分
考點:本題主要考查立體幾何中的垂直關系,角的計算。
點評:典型題,立體幾何題,是高考必考內容,往往涉及垂直關系、平行關系、角、距離、體積的計算。在計算問題中,有“幾何法”和“向量法”。利用幾何法,要遵循“一作、二證、三計算”的步驟,利用空間向量,省去繁瑣的證明,也是解決立體幾何問題的一個基本思路。注意運用轉化與化歸思想,將空間問題轉化成平面問題。本題利用空間向量知識解答,關鍵點是建立適當地空間直角坐標系。


科目:高中數學 來源:2011屆甘肅省蘭州一中高三第三次模擬考試理科數學 題型:解答題
(本小題滿分12分)
如圖,四棱柱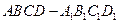 中,
中,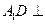 平面
平面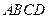 ,底面
,底面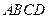 是邊長為
是邊長為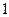 的正方形,側棱
的正方形,側棱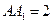 .
.
(1)求證: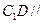 平面
平面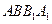 ;
;
(2)求直線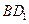 與平面
與平面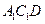 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省泉州市畢業(yè)班(第二輪)質量檢測理科數學試卷(解析版) 題型:解答題
如圖,四棱柱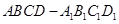 中,
中,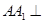 平面
平面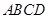 .
.

(Ⅰ)從下列①②③三個條件中選擇一個做為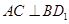 的充分條件,并給予證明;
的充分條件,并給予證明;
①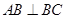 ,②
,②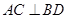 ;③
;③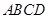 是平行四邊形.
是平行四邊形.
(Ⅱ)設四棱柱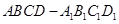 的所有棱長都為1,且
的所有棱長都為1,且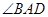 為銳角,求平面
為銳角,求平面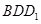 與平面
與平面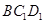 所成銳二面角
所成銳二面角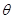 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三第七次階段復習達標檢測理科數學試卷(解析版) 題型:解答題
如圖,四棱柱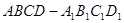 中,
中,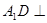 平面
平面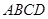 ,底面
,底面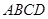 是邊長為1的正方形,側棱
是邊長為1的正方形,側棱 ,
,
(Ⅰ)證明: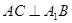 ;
;
(Ⅱ)若棱 上存在一點
上存在一點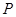 ,使得
,使得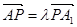 ,
,
當二面角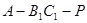 的大小為
的大小為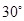 時,求實數
時,求實數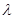 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年甘肅省高三第三次模擬考試理科數學 題型:解答題
(本小題滿分12分)
如圖,四棱柱 中,
中, 平面
平面 ,底面
,底面 是邊長為
是邊長為 的正方形,側棱
的正方形,側棱 .
.

(1)求證: 平面
平面 ;
;
(2)求直線 與平面
與平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com