(本小題滿分12分)
已知等差數(shù)列
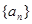
的公差
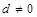
,設
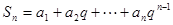
,
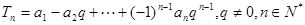
(Ⅰ)若
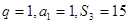
,求數(shù)列
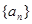
的通項公式;
(Ⅱ)若
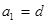
,且
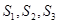
成等比數(shù)列,求
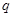
的值;
(Ⅲ)若
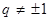
,證明:
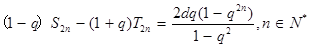
.
本試題主要是考查了數(shù)列的通項公式和數(shù)列求和的運用。
(1)由題設,
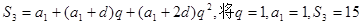
代入解得
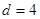
,得到其通項公式。
(2)因為
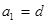
,且
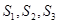
成等比數(shù)列,所以
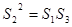
,
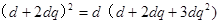
,化簡得到結(jié)論
(3)由題設,可得
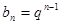
,然后運用錯位相減法得到數(shù)列的求和。
(1)解:由題設,
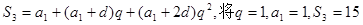
代入解得
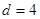
,所以
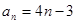
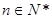
(2)解:當
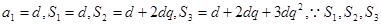
成等比數(shù)列,所以
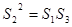
,即
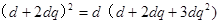
,注意到
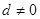
,整理得
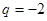
(3)證明:由題設,可得
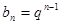
,則
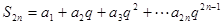
①
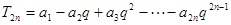
②
①-②得,
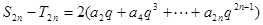
①+②得,
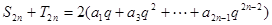
③
③式兩邊同乘以 q,得
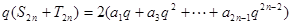
所以
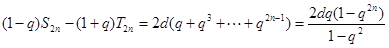
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
某工廠2009年生產(chǎn)某種產(chǎn)品2萬件,計劃從2010年起每年比上一年增長20%,這個工廠年產(chǎn)量超過12萬的最早的一年是(注:lg2=0.3010,lg3=0.4771)
| A.2018年 | B.2019年 | C.2020年 | D.2021年 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
某人
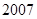
年
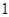
月
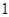
日到銀行存入一年期存款
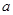
元,若按年利率為
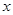
,并按復利計算,到
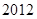
年
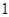
月
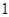
日可取回的款共
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
等差數(shù)列
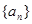
的前n項和記為

,已知
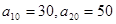
.
(1)求通項
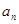
;
(2)若

=242,求n。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知數(shù)列{a
n}為正項等比數(shù)列,其前

項和為
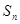
,若
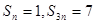
,則
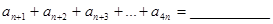
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
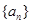
是公比大于1的等比數(shù)列,
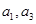
是函數(shù)
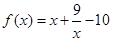
的兩個零點。
(1)求數(shù)列
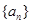
的通項公式;
(2)若數(shù)列

滿足
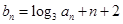
,且
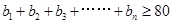
,求
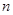
的最小值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在等比數(shù)列
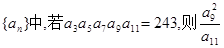
的值為( )
查看答案和解析>>

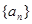 的公差
的公差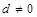 ,設
,設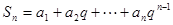 ,
,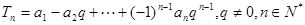
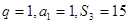 ,求數(shù)列
,求數(shù)列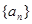 的通項公式;
的通項公式;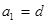 ,且
,且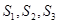 成等比數(shù)列,求
成等比數(shù)列,求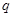 的值;
的值;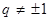 ,證明:
,證明: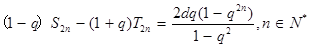 .
.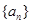 是公比大于1的等比數(shù)列,
是公比大于1的等比數(shù)列,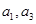 是函數(shù)
是函數(shù)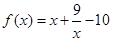 的兩個零點。
的兩個零點。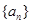 的通項公式;
的通項公式; 滿足
滿足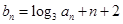 ,且
,且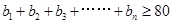 ,求
,求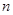 的最小值。
的最小值。