
已知數列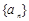 滿足
滿足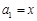 ,
,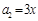 ,
,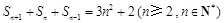 ,
,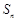 是數列
是數列 的前
的前 項和.
項和.
(1)若數列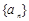 為等差數列.
為等差數列.
(ⅰ)求數列的通項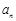 ;
;
(ⅱ)若數列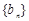 滿足
滿足 ,數列
,數列 滿足
滿足 ,試比較數列
,試比較數列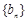 前
前 項和
項和 與
與 前
前 項和
項和 的大小;
的大小;
(2)若對任意 ,
,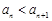 恒成立,求實數
恒成立,求實數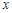 的取值范圍.
的取值范圍.
(1)(ⅰ)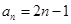 ;(ⅱ)詳見解析;(2)
;(ⅱ)詳見解析;(2)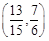 .
.
解析試題分析:(1)(ⅰ)由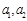 可得
可得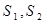 ,在遞推關系式
,在遞推關系式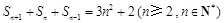 中,由
中,由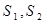 可求
可求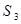 ,進而求出
,進而求出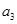 ,于是可利用
,于是可利用 是等差數列求出
是等差數列求出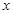 的值,最后可求出
的值,最后可求出 的通項公式,(ⅱ)易知
的通項公式,(ⅱ)易知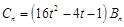 ,所以要比較
,所以要比較 和
和 的大小,只需確定
的大小,只需確定 的符號和
的符號和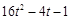 和1的大小關系問題,前者易知為正,后者作差后判斷符號即可;(2)本題可由遞推關系式
和1的大小關系問題,前者易知為正,后者作差后判斷符號即可;(2)本題可由遞推關系式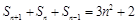 通過變形得出
通過變形得出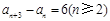 ,于是可以看出任意
,于是可以看出任意 ,
,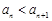 恒成立,須且只需
恒成立,須且只需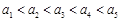 ,從而可以求出
,從而可以求出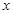 的取值范圍.
的取值范圍.
試題解析:(1)(ⅰ)因為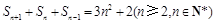 ,所以
,所以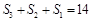 ,
,
即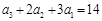 ,又
,又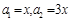 ,所以
,所以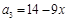 , 2分
, 2分
又因為數列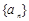 成等差數列,所以
成等差數列,所以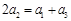 ,即
,即 ,解得
,解得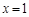 ,
,
所以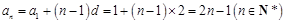 ; 4分
; 4分
(ⅱ)因為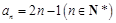 ,所以
,所以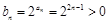 ,其前
,其前 項和
項和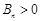 ,
,
又因為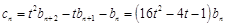 , 5分
, 5分
所以其前 項和
項和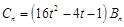 ,所以
,所以 , 7分
, 7分
當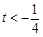 或
或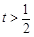 時,
時,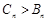 ;當
;當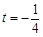 或
或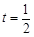 時,
時,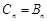 ;
;
當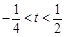 時,
時,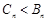 . 9分
. 9分
(2)由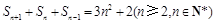 知
知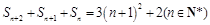 ,
,
兩式作差,得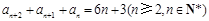 , 10分
, 10分
所以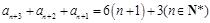 ,
,
再作差得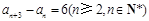 , 11分
, 11分
所以,當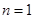 時,
時,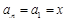 ;
;
當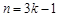 時,
時,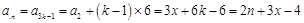 ;
;
當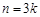 時,
時,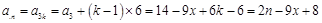 ;
;
當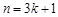 時,
時,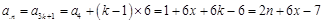 ; 14分
; 14分
因為對任意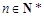 ,
,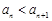 恒成立,所以
恒成立,所以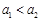 且
且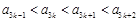 ,
,
所以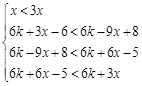 ,解得,
,解得,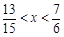 ,故實數
,故實數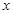 的取值范圍為
的取值范圍為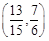


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:解答題
已知Sn是等比數列{an}的前n項和,S4,S2,S3成等差數列,且a2+a3+a4=-18.
(1)求數列{an}的通項公式;
(2)是否存在正整數n,使得Sn≥2 013?若存在,求出符合條件的所有n的集合;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知各項均不相等的等差數列{an}的前5項和為S5=35,且a1+1,a3+1,a7+1成等比數列.
(1)求數列{an}的通項公式;
(2)設Tn為數列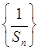 的前n項和,問是否存在常數m,使Tn=m
的前n項和,問是否存在常數m,使Tn=m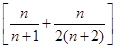 ,若存在,求m的值;若不存在,說明理由.
,若存在,求m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設數列{an}滿足an+1=2an+n2-4n+1.
(1)若a1=3,求證:存在 (a,b,c為常數),使數列{an+f(n)}是等比數列,并求出數列{an}的通項公式;
(a,b,c為常數),使數列{an+f(n)}是等比數列,并求出數列{an}的通項公式;
(2)若an是一個等差數列{bn}的前n項和,求首項a1的值與數列{bn}的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com