
定義函數(shù) 其導(dǎo)函數(shù)記為
其導(dǎo)函數(shù)記為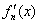 .
.
(1) 求證: ;
;
(2) 設(shè)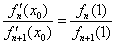 ,求證:
,求證: ;
;
(3) 是否存在區(qū)間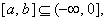 使函數(shù)
使函數(shù) 在區(qū)間
在區(qū)間 上的值域?yàn)?sub>
上的值域?yàn)?sub>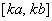 ?
若存在,求出最小的
?
若存在,求出最小的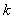 值及相應(yīng)的區(qū)間
值及相應(yīng)的區(qū)間 .
.
(1)∵ ,令
,令
則
當(dāng) 時(shí)
時(shí) ,當(dāng)
,當(dāng) 時(shí),
時(shí),
∴ 在
在 上遞減,在
上遞減,在 上遞增
上遞增
故 在
在 處取得極(最)小值
處取得極(最)小值
∴ ,即
,即 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) 時(shí)取等號(hào))……………………4分
時(shí)取等號(hào))……………………4分
(2)由 ,得
,得
∴ ,
, ,易知
,易知 ,…………….6分
,…………….6分
而
由(1)知當(dāng) 時(shí),
時(shí), ,故
,故
∴ ,∴
,∴ …………………………………………………………9分
…………………………………………………………9分
(3)

 令
令 ,得
,得 或
或 ,
,
∴當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ,
,
故 的圖象如圖所示。
的圖象如圖所示。
下面考查直線 與
與 的相交問(wèn)題
的相交問(wèn)題
由圖可知直線 與
與 存在交點(diǎn),
存在交點(diǎn),
且滿足 在區(qū)間
在區(qū)間 上的值域?yàn)?sub>
上的值域?yàn)?sub>
∵在 上,
上, 為圖象的極小值點(diǎn)
為圖象的極小值點(diǎn)
∴過(guò) 作直線
作直線 與
與 的圖象交于另一點(diǎn)
的圖象交于另一點(diǎn) ,當(dāng)直線
,當(dāng)直線 繞原點(diǎn)
繞原點(diǎn) 順時(shí)鐘旋轉(zhuǎn)至點(diǎn)
順時(shí)鐘旋轉(zhuǎn)至點(diǎn) 時(shí),滿足條件的
時(shí),滿足條件的 取最小值,即
取最小值,即 的最小值為
的最小值為 ,相應(yīng)區(qū)間
,相應(yīng)區(qū)間 為
為 。…………………………………………………………………………
。…………………………………………………………………………


 數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案
數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:湖南省2007屆高三十校聯(lián)考第一次考試?yán)砜茢?shù)學(xué)試卷 題型:044
定義函數(shù)![]() 其導(dǎo)函數(shù)記為
其導(dǎo)函數(shù)記為![]() .
.
(1)求證:fn(x)≥nx;
(2)設(shè)![]() ,求證:0<x0<1;
,求證:0<x0<1;
(3)是否存在區(qū)間![]() 使函數(shù)h(x)=f3(x)-f2(x)在區(qū)間[a,b]上的值域?yàn)閇ka,kb]?若存在,求出最小的k值及相應(yīng)的區(qū)間[a,b].
使函數(shù)h(x)=f3(x)-f2(x)在區(qū)間[a,b]上的值域?yàn)閇ka,kb]?若存在,求出最小的k值及相應(yīng)的區(qū)間[a,b].
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省高三第八次月考理科數(shù)學(xué)試卷 題型:解答題
定義函數(shù)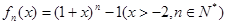 其導(dǎo)函數(shù)記為
其導(dǎo)函數(shù)記為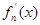 .
.
(Ⅰ)求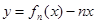 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅱ)若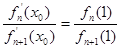 ,求證:
,求證: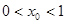 ;
;
(Ⅲ)設(shè)函數(shù)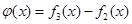 ,數(shù)列
,數(shù)列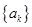 前
前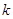 項(xiàng)和為
項(xiàng)和為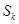 ,
, 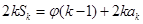 ,其中
,其中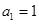 .對(duì)于給定的正整數(shù)
.對(duì)于給定的正整數(shù) ,數(shù)列
,數(shù)列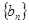 滿足
滿足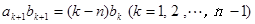 ,且
,且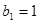 ,求
,求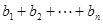 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
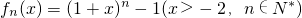 其導(dǎo)函數(shù)記為
其導(dǎo)函數(shù)記為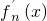 .
.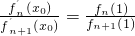 ,求證:0<x0<1;
,求證:0<x0<1;查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:福建省龍巖一中2011-2012學(xué)年高三下學(xué)期第八次月考試卷數(shù)學(xué)(理) 題型:解答題
定義函數(shù)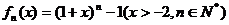 其導(dǎo)函數(shù)記為
其導(dǎo)函數(shù)記為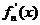 .
.
(Ⅰ)求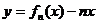 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅱ)若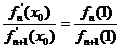 ,求證:
,求證: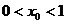 ;
;
(Ⅲ)設(shè)函數(shù)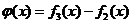 ,數(shù)列
,數(shù)列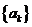 前
前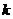 項(xiàng)和為
項(xiàng)和為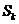 ,
,
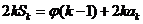 ,其中
,其中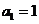 .對(duì)于給定的正整數(shù)
.對(duì)于給定的正整數(shù)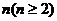 ,數(shù)列
,數(shù)列 滿足
滿足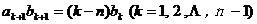 ,且
,且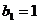 ,求
,求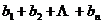 .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com