
 的圖像經過點
的圖像經過點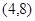 .
.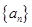 中,若
中,若 ,
,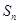 為數列
為數列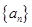 的前
的前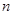 項和,且滿足
項和,且滿足 ,
,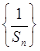 成等差數列,并求數列
成等差數列,并求數列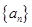 的通項公式;
的通項公式;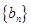 ,若將數列
,若將數列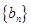 中的所有項按每一行比上一行多一項的規則排成
中的所有項按每一行比上一行多一項的規則排成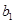 |
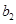 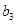 |
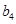 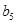 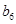 |
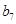 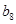  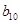 |
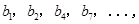 構成的數列即為數列
構成的數列即為數列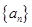 ,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當
,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當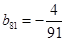 時,求上表中第
時,求上表中第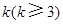 行所有項的和.
行所有項的和.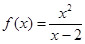 .(2)
.(2)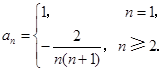
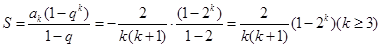 .
.  的圖像經過點
的圖像經過點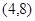 得:
得: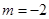 ,
,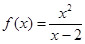
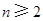 時,
時,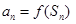 ,即
,即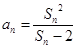 .
.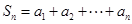 ,
,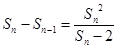 ,即
,即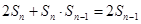 ,
,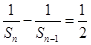 得到通項公式。
得到通項公式。 ,且
,且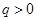 .
.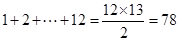 ,
,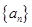 的前78項,
的前78項,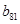 在表中第13行第三列,然后利用數列的公式得到求解。
在表中第13行第三列,然后利用數列的公式得到求解。 的圖像經過點
的圖像經過點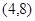 得:
得: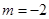 ,
,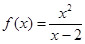 . …………..2分
. …………..2分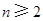 時,
時,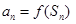 ,即
,即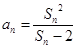 .
.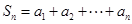 ,
,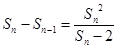 ,即
,即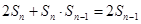 ,……………..5分
,……………..5分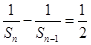 , ……………………..7分
, ……………………..7分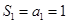 .
.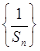 是首項為1,公差為
是首項為1,公差為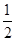 的等差數列.
的等差數列.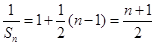 ,即
,即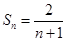 .
.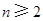 時,
時,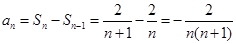 .
.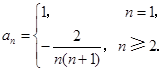 ……………………..9分
……………………..9分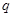 ,且
,且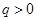 .
.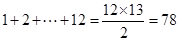 ,
,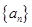 的前78項,
的前78項,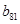 在表中第13行第三列, ……………………..11分
在表中第13行第三列, ……………………..11分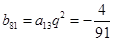 .
.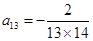 , 所以
, 所以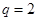 . ……………………..13分
. ……………………..13分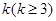 行所有項的和為
行所有項的和為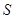 ,
,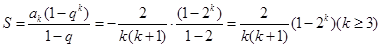 .…..16分
.…..16分

科目:高中數學 來源:不詳 題型:解答題
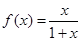
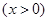 ,數列
,數列 滿足:
滿足: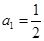 ,
,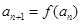
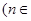 N*
N*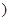 .
. 的通項公式;
的通項公式;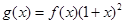 ,數列
,數列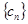 滿足:
滿足: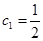 ,
,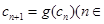 N*),
N*), 的正整數,都滿足:
的正整數,都滿足: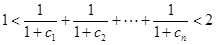 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
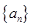 是首項為
是首項為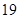 ,公差為
,公差為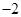 的等差數列,
的等差數列,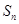 為
為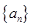 的前
的前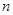 項和.
項和.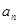 及
及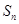 ;
;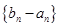 是首項為1,公比為3的等比數列,求數列
是首項為1,公比為3的等比數列,求數列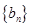 的通項公式及其前
的通項公式及其前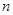 項和
項和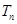 .
. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com