
已知數列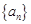 滿足:
滿足: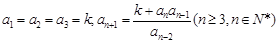 其中
其中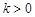 ,數列
,數列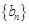 滿足:
滿足: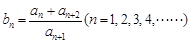
(1)求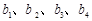 ;
;
(2)求數列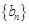 的通項公式;
的通項公式;
(3)是否存在正數k,使得數列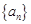 的每一項均為整數,如果不存在,說明理由,如果存在,求出所有的k.
的每一項均為整數,如果不存在,說明理由,如果存在,求出所有的k.
(1)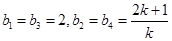 (2)
(2)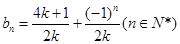 (3)
(3)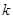 的取值集合是
的取值集合是
解析試題分析:(1)先由遞推公式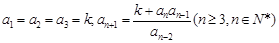 求出
求出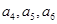
再用遞推公式求出 ;
;
(2)由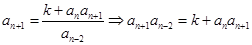
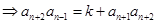
兩式相減可得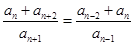 即:
即: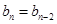 ,于是結合(1)的結論可得
,于是結合(1)的結論可得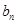 .
.
(3)對于這類問題通常的做法是假設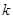 的值存在,由(1)的結果知,
的值存在,由(1)的結果知,
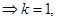 或
或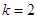 ,接下來可用數學歸納法證明結論成立即可.
,接下來可用數學歸納法證明結論成立即可.
試題解析:(1)經過計算可知: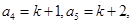
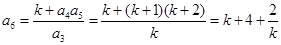 .
.
求得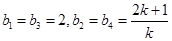 . (4分)
. (4分)
(2)由條件可知: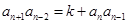 . ①
. ①
類似地有: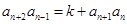 . ②
. ②
①-②有: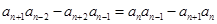 .
.
即: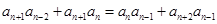 .
. 因此:
因此:
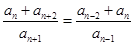
即: 故
故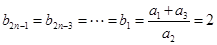
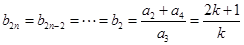
所以: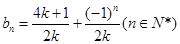 . (8分)
. (8分)
(3)假設存在正數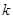 ,使得數列
,使得數列 的每一項均為整數.
的每一項均為整數.
則由(2)可知: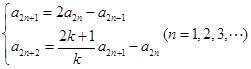 ③
③
由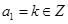 ,及
,及 可知
可知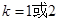 .
.
當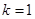 時,
時,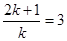 為整數,利用
為整數,利用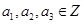 ,結合③式,反復遞推,可知
,結合③式,反復遞推,可知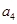 ,
,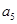 ,
,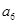 ,
,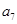 , 均為整數.
, 均為整數.
當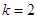 時,③變?yōu)?img src="http://thumb.zyjl.cn/pic5/tikupic/79/4/eskdb1.png" style="vertical-align:middle;" /> ④
時,③變?yōu)?img src="http://thumb.zyjl.cn/pic5/tikupic/79/4/eskdb1.png" style="vertical-align:middle;" /> ④
我們用數學歸納法證明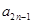 為偶數,
為偶數,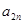 為整數
為整數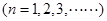
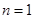 時,結論顯然成立,假設
時,結論顯然成立,假設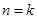 時結論成立,這時
時結論成立,這時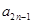 為偶數,
為偶數,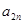 為整數,故
為整數,故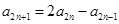 為偶數,
為偶數, 為整數,所以
為整數,所以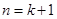 時,命題成立.
時,命題成立.
故數列 是整數列.
是整數列.
綜上所述,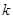 的取值集合是
的取值集合是 . (14分)
. (14分)
考點:1、數列的遞推公式;2、數學歸納法.


 時刻準備著暑假作業(yè)原子能出版社系列答案
時刻準備著暑假作業(yè)原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業(yè)暑假成長樂園新疆青少年出版社系列答案
假期作業(yè)暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
已知數列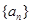 和
和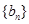 的通項公式分別為
的通項公式分別為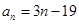 ,
,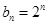 .將
.將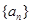 與
與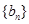 中的公共項按照從小到大的順序排列構成一個新數列記為
中的公共項按照從小到大的順序排列構成一個新數列記為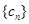 .
.
(1)試寫出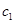 ,
,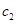 ,
,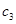 ,
,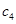 的值,并由此歸納數列
的值,并由此歸納數列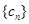 的通項公式;
的通項公式;
(2)證明你在(1)所猜想的結論.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com