
如圖,四棱錐 中,底面是以
中,底面是以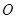 為中心的菱形,
為中心的菱形, 底面
底面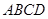 ,
,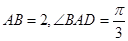 ,
, 為
為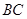 上一點,且
上一點,且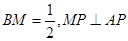 .
.
(1)求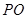 的長;
的長;
(2)求二面角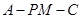 的正弦值.
的正弦值.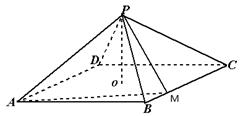
(1)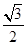 ;(2)
;(2)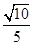 .
.
解析試題分析:(1)連結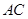 、
、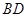 ,因為是菱形
,因為是菱形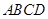 的中心,
的中心,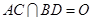 ,以
,以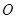 為坐標原點,
為坐標原點,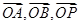 的方向分別為
的方向分別為 軸、
軸、 軸、
軸、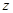 軸的正方向,建立空間直角坐標系,根據題設條件寫出
軸的正方向,建立空間直角坐標系,根據題設條件寫出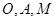 的坐標,并設出點
的坐標,并設出點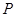 的坐標
的坐標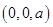 ,根據空間兩點間的距離公式和勾股定理列方程解出
,根據空間兩點間的距離公式和勾股定理列方程解出 的值得到
的值得到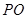 的長;.
的長;.
(2)設平面 的法向量為
的法向量為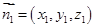 ,平面PMC的法向量為
,平面PMC的法向量為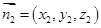 ,首先利用向量的數量積列方程求出向量
,首先利用向量的數量積列方程求出向量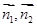 的坐標,再利用向量的夾角公式求出
的坐標,再利用向量的夾角公式求出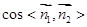 ,進而求出二面角
,進而求出二面角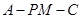 的正弦值.
的正弦值.
解: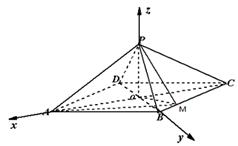
(1)如圖,連結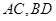 ,因
,因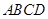 為菱形,則
為菱形,則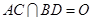 ,且
,且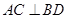 ,以
,以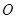 為坐標原點,
為坐標原點,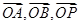 的方向分別為
的方向分別為 軸,
軸, 軸,
軸,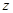 軸的正方向,建立空間直角坐標系
軸的正方向,建立空間直角坐標系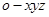 ,
,
因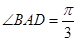 ,故
,故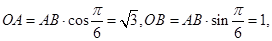
所以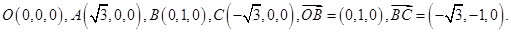
由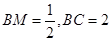 知,
知,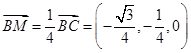
從而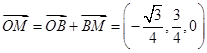 ,即
,即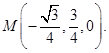
設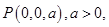 ,則
,則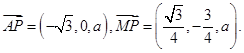 因為
因為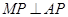 ,
,
故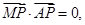 即
即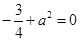 ,所以
,所以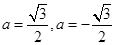 (舍去),即
(舍去),即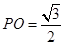 .
.
(2)由(1)知, ,
,
設平面 的法向量為
的法向量為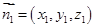 ,平面
,平面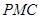 的法向量為
的法向量為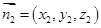
由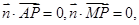 得
得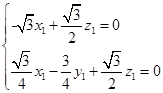 故可取
故可取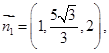
由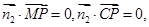 得
得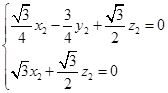 故可取
故可取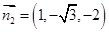
從而法向量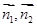 的夾角的余弦值為
的夾角的余弦值為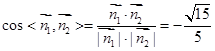
故所求二面角 的正弦值為
的正弦值為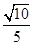 .
.
考點:1、空間直線與平面垂直的性質;2、空間直角坐標系;3、空間向量的數量積及其應用.


科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E為PC的中點.
(1)求證:BE∥平面PAD;
(2)求二面角E-BD-C的余弦值.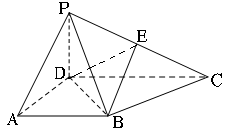
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐E﹣ABCD中,矩形ABCD所在的平面與平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分別為BE,AE,BC的中點
(1)求證:DE∥平面FGH;
(2)若點P在直線GF上,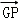 =λ
=λ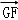 ,且二面角D﹣BP﹣A的大小為
,且二面角D﹣BP﹣A的大小為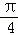 ,求λ的值.
,求λ的值.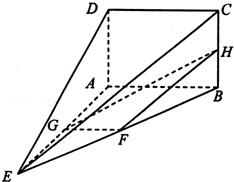
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在梯形ABCD中,AB//CD,AD=DC=CB=a,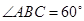 ,平面
,平面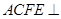 平面ABCD,四邊形ACFE是矩形,AE=a.
平面ABCD,四邊形ACFE是矩形,AE=a.
(1)求證: 平面ACFE;
平面ACFE;
(2)求二面角B—EF—D的平面角的余弦值.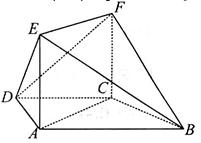
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,四棱錐P-ABCD中,PA⊥平面ABCD,E為BD的中點,G為PD的中點,△DAB ≌△DCB,EA=EB=AB=1,PA= ,連接CE并延長交AD于F.
,連接CE并延長交AD于F.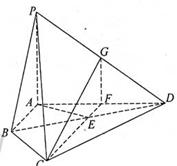
(1)求證:AD⊥平面CFG;
(2)求平面BCP與平面DCP的夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E是棱AB上的動點.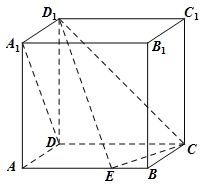
(1)求證:DA1⊥ED1;
(2)若直線DA1與平面CED1成角為45o,求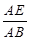 的值;
的值;
(3)寫出點E到直線D1C距離的最大值及此時點E的位置(結論不要求證明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com