
已知函數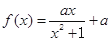 ,
,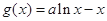 (
(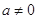 ).
).
(1)求函數 的單調區間;
的單調區間;
(2)求證:當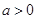 時,對于任意
時,對于任意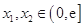 ,總有
,總有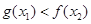 成立.
成立.
(1)當 時,
時, 的單調遞增區間為
的單調遞增區間為 ,單調遞減區間為
,單調遞減區間為 ,
, ;當
;當 時,
時, 的單調遞增區間為
的單調遞增區間為 ,
, ,單調遞減區間為
,單調遞減區間為 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)對于含參數的函數的單調區間,只需在定義域內考慮導函數符號,同時要注意分類討論標準的確定.先求
科目:高中數學
來源:
題型:解答題
定義在
科目:高中數學
來源:
題型:解答題
(14分)己知函數f (x)=ex,x
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 ,分母恒正,只需考慮分子二次函數的符號,所以討論開口方向即可;(2)由于
,分母恒正,只需考慮分子二次函數的符號,所以討論開口方向即可;(2)由于 是獨立的兩個變量,故
是獨立的兩個變量,故 分別代表
分別代表 ,
, 的任意兩個函數值,要使得
的任意兩個函數值,要使得 恒成立,只需證明
恒成立,只需證明 ,分別利用導數求其最大值和最小值,從而得證,該題入手,可能很多同學困惑于
,分別利用導數求其最大值和最小值,從而得證,該題入手,可能很多同學困惑于 這兩個變量的處理,從而造成了解題障礙.
這兩個變量的處理,從而造成了解題障礙.
試題解析:(Ⅰ)函數 的定義域為
的定義域為 ,
, .
.
當 時,
時,
當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表:
當







0 
0 

↘ ↗ ↘  時,
時,
當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表:


中考研究全國各省市中考真題單元專題訓練系列答案
中考風向標系列答案
創新教程系列答案
互動中考復習大講義系列答案
中考階段總復習ABC系列答案
達優測試卷系列答案
劍指中考系列答案
名師點睛教材詳解系列答案
課堂精練解讀與指導系列答案
初中語文閱讀專題訓練系列答案
 上的函數
上的函數 同時滿足以下條件:
同時滿足以下條件:
① 在(0,1)上是減函數,在(1,+∞)上是增函數;
在(0,1)上是減函數,在(1,+∞)上是增函數;
② 是偶函數;
是偶函數;
③ 在x=0處的切線與直線
在x=0處的切線與直線 y=x+2垂直.
y=x+2垂直.
(1)求函數 =
= 的解析式;
的解析式;
(2)設g(x)= ,若存在實數x∈[1,e],使
,若存在實數x∈[1,e],使 <
< ,求實數m的取值范圍.
,求實數m的取值范圍. R
R
(1)求 f (x)的反函數圖象上點(1,0)處的切線方程。
(2)證明:曲線y=f(x)與曲線y=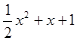 有唯一公共點;
有唯一公共點;
(3)設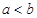 ,比較
,比較 與
與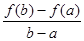 的大小,并說明理由。
的大小,并說明理由。 (k為常數,e=2.71828……是自然對數的底數),曲線
(k為常數,e=2.71828……是自然對數的底數),曲線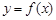 在點
在點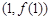 處的切線與x軸平行。
處的切線與x軸平行。
(1)求k的值;
(2)求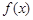 的單調區間;
的單調區間;
(3)設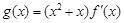 ,其中
,其中 為
為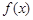 的導函數,證明:對任意
的導函數,證明:對任意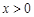 ,
, 。
。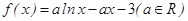 .
.
(I)若 ,求函數
,求函數 的單調區間;
的單調區間;
(Ⅱ)求證: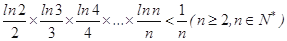
(Ⅲ)若函數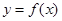 的圖象在點
的圖象在點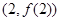 處的切線的傾斜角為
處的切線的傾斜角為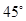 ,對于任意的
,對于任意的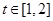 ,函數
,函數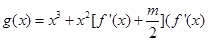 是
是 的導函數)在區間
的導函數)在區間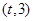 上總不是單調函數,求
上總不是單調函數,求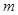 的取值范圍。
的取值范圍。
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號