
已知函數 (k為常數,e=2.71828……是自然對數的底數),曲線
(k為常數,e=2.71828……是自然對數的底數),曲線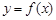 在點
在點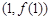 處的切線與x軸平行。
處的切線與x軸平行。
(1)求k的值;
(2)求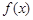 的單調區間;
的單調區間;
(3)設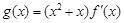 ,其中
,其中 為
為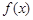 的導函數,證明:對任意
的導函數,證明:對任意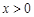 ,
, 。
。
(1) ;(2)單調遞增區間為
;(2)單調遞增區間為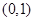 ,單調遞減區間為
,單調遞減區間為 ;(3)詳見解析.
;(3)詳見解析.
解析試題分析:(1)先求導函數 ,由導數的幾何意義得
,由導數的幾何意義得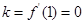 ,列方程求
,列方程求 ;(2)求
;(2)求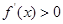 的解集和定義域求交集,得單調遞增區間;求
的解集和定義域求交集,得單調遞增區間;求 的解集并和定義域求交集,得單調遞減區間,該題
的解集并和定義域求交集,得單調遞減區間,該題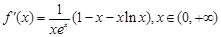 ,可觀察當
,可觀察當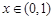 時,
時,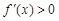 ;
; 時,
時, .所以單調區間可求;(3)
.所以單調區間可求;(3)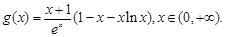 思路一:考慮
思路一:考慮 的最大值,證明最大值小于
的最大值,證明最大值小于 即可,但是考慮到解析式的復雜性,可對不等式等價變形;思路二:原不等式等價于
即可,但是考慮到解析式的復雜性,可對不等式等價變形;思路二:原不等式等價于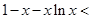
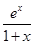
 ,記
,記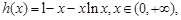 ,利用導數可求其最大值為
,利用導數可求其最大值為 ,從圖象可以判斷
,從圖象可以判斷 的圖象在直線
的圖象在直線 的上方,也就是說
的上方,也就是說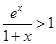 恒成立,故
恒成立,故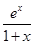

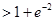 ,所以命題得證.
,所以命題得證.
試題解析:(Ⅰ)由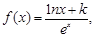 得
得 由于曲線
由于曲線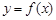 在
在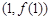 處的切線與x軸平行,所以
處的切線與x軸平行,所以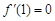 ,因此
,因此
(Ⅱ)由(Ⅰ)得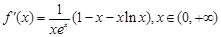 ,令
,令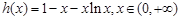 當
當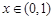 時,
時,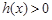 ;當
;當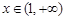 時,
時,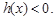 又
又 ,所以
,所以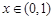 時,
時,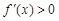 ;
; 時,
時, . 因此
. 因此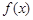 的單調遞增區間為(0,1),單調遞減區間
的單調遞增區間為(0,1),單調遞減區間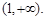
(Ⅲ)證明因為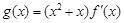 ,所以
,所以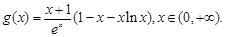 因此對任意
因此對任意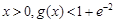 等價于
等價于 由(Ⅱ)知
由(Ⅱ)知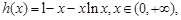
所以 因此當
因此當 時,
時,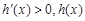 單調遞增;當
單調遞增;當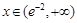 時
時 單調遞增. 所以
單調遞增. 所以 的最大值為
的最大值為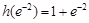 故
故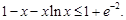 設
設 因為
因為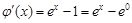 ,所以
,所以 時,
時, 單調遞增,
單調遞增,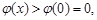
故 時,
時,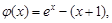 即
即 所以
所以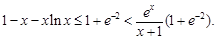 因此對任意
因此對任意
考點:1、導數的幾何意義;2、導數 在單調性上的應用;3、利用導數求函數的最值.


科目:高中數學 來源: 題型:解答題
已知函數 ,
, .
.
(1)若 ,則
,則 ,
, 滿足什么條件時,曲線
滿足什么條件時,曲線 與
與 在
在 處總有相同的切線?
處總有相同的切線?
(2)當 時,求函數
時,求函數 的單調減區間;
的單調減區間;
(3)當 時,若
時,若 對任意的
對任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數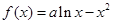 .
.
(1)當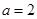 時,求函數
時,求函數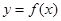 在
在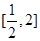 上的最大值;
上的最大值;
(2)令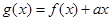 ,若
,若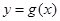 在區間
在區間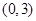 上不單調,求
上不單調,求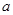 的取值范圍;
的取值范圍;
(3)當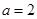 時,函數
時,函數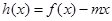 的圖象與
的圖象與 軸交于兩點
軸交于兩點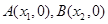 ,且
,且 ,又
,又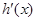 是
是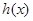 的導函數.若正常數
的導函數.若正常數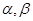 滿足條件
滿足條件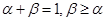 .證明:
.證明: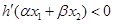 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區注重生態環境建設,每年用于改造生態環境總費用為 億元,其中用于風景區改造為
億元,其中用于風景區改造為 億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用
億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用 隨每年改造生態環境總費用
隨每年改造生態環境總費用 增加而增加;②每年改造生態環境總費用至少
增加而增加;②每年改造生態環境總費用至少 億元,至多
億元,至多 億元;③每年用于風景區改造費用
億元;③每年用于風景區改造費用 不得低于每年改造生態環境總費用
不得低于每年改造生態環境總費用 的15%,但不得高于每年改造生態環境總費用
的15%,但不得高于每年改造生態環境總費用 的25%.
的25%.
若 ,
, ,請你分析能否采用函數模型y=
,請你分析能否采用函數模型y=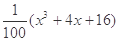 作為生態環境改造投資方案.
作為生態環境改造投資方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com