中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

在⊿ABC中，角A，B，C的對邊分別為A,b,C,且滿足(2A-C)CosB=bCosC.
(Ⅰ)求角B的大小；
(Ⅱ)已知函數f(A,C)=Cos2A+sin2C,求f(A,C)的最大值。

(Ⅰ);(Ⅱ)1+.

解析試題分析：（1）利用正弦定理，結合A、B的范圍求出求角B的大小；(Ⅱ)把C用A來表示，在＝１時取最大值.
試題解析：(Ⅰ)∵ (2A-C)CosB=bCosC　　∴ 由正弦定理得
又∵  ∴ 
(Ⅱ)


考點：1、正弦定理的應用；2、三角函數的最值．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

已知向量，，設函數，.
（Ⅰ）求的最小正周期與最大值；
（Ⅱ）在中，分別是角的對邊，若的面積為，求的值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

設函數f(θ)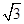＝sinθ＋cosθ，其中，角θ的頂點與坐標原點重合，始邊與x軸非負半軸重合，終邊經過點P(x，y)，且0≤θ≤π.
(1)若點P的坐標為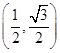，求f(θ)的值；
(2)若點P(x，y)為平面區域Ω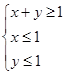：，上的一個動點，試確定角θ的取值范圍，并求函數f(θ)的最小值和最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

設函數f（x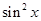）＝－sin（2x－）．
（I）求函數f（x）的最大值和最小值；
（Ⅱ）△ABC的內角A，B，C的對邊分別為a，b，c，c＝3，f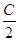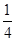（）＝，若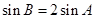，求△ABC的面積．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

設函數的最大值為，最小值為，其中．
（1）求、的值（用表示）；
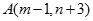（2）已知角的頂點與平面直角坐標系中的原點重合，始邊與軸的正半軸重合，終邊經過點．求的值．  

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（1）設，求的值；
（2）已知，且，求的值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在銳角中，.
（Ⅰ）求角的大小；
（Ⅱ）求的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在中，角所對的邊分別為，且.
（Ⅰ）求函數的最大值；
（Ⅱ）若，，，求的值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知向量向量與向量的夾角為，且.
（1）求向量 ；  
（2）若向量與共線，向量，其中、為的內角，且、、依次成等差數列，求的取值范圍．

查看答案和解析>>

同步練習冊答案