
已知函數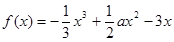 ,
,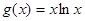
(Ⅰ)當a=4時,求函數f(x)的單調區間;
(Ⅱ)求函數g(x)在區間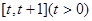 上的最小值;
上的最小值;
(Ⅲ)若存在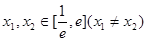 ,使方程
,使方程
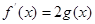 成立,求實數a的取值范圍(其中e=2.71828是自然對數的底數)
成立,求實數a的取值范圍(其中e=2.71828是自然對數的底數)
(Ⅰ)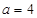 時,
時,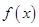 的單調增區間為
的單調增區間為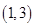 ,單調減區間為
,單調減區間為 .
.
(Ⅱ)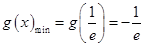 ;(III)實數
;(III)實數 的取值范圍為
的取值范圍為 .
.
解析試題分析:(Ⅰ)求導數,根據
科目:高中數學
來源:
題型:解答題
如圖,現要在邊長為
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
已知數列
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區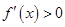 ,
,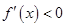 得到函數的單調區間.
得到函數的單調區間.
(Ⅱ)遵循“求導數,求駐點,討論單調性,確定最值”.
(III) 由 可得
可得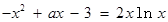
“分離參數”得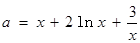 .
.
令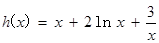 ,遵循“求導數,求駐點,討論單調性,確定最值”.
,遵循“求導數,求駐點,討論單調性,確定最值”.
“表解法”往往直觀易懂,避免出錯.
試題解析:(Ⅰ)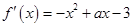 1分
1分
當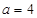 時,
時, 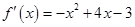 ,令
,令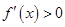 得
得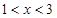 2分
2分
∴當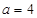 時,
時,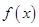 的單調增區間為
的單調增區間為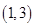 ,單調減區間為
,單調減區間為 . 3分
. 3分
(Ⅱ)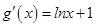 , 令
, 令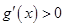 ,得
,得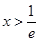 4分
4分
①當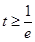 時,在區間
時,在區間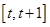 上
上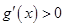 ,
, 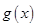 為增函數,
為增函數,
∴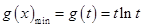 5分
5分
②當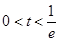 時,在區間
時,在區間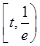 上
上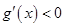 ,
,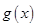 為減函數, 6分
為減函數, 6分
在區間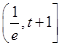 上
上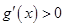 ,
,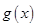 為增函數, 7分
為增函數, 7分
∴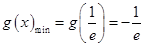 8分
8分
(III) 由 可得
可得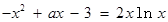
∴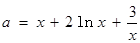 , 9分
, 9分
令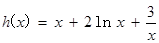 ,則
,則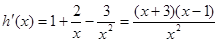 10分
10分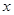
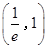
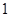
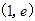
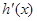
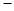

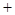
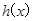
單調遞減 

中考新航標初中重點知識總復習指導系列答案
金點新課標同步精練系列答案
教材精析精練字詞句篇系列答案
上海中考總動員系列答案

新課標應用題系列答案
通城學典拓展閱讀訓練系列答案
單元自測試卷青島出版社系列答案
天利38套小升初特訓卷系列答案
時事政治系列答案
 的正方形
的正方形 內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為
內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為 (
( 不小于
不小于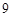 )的扇形花壇,以正方形的中心為圓心建一個半徑為
)的扇形花壇,以正方形的中心為圓心建一個半徑為 的圓形草地.為了保證道路暢通,島口寬不小于
的圓形草地.為了保證道路暢通,島口寬不小于 ,繞島行駛的路寬均不小于
,繞島行駛的路寬均不小于 .
.
(1)求 的取值范圍;(運算中
的取值范圍;(運算中 取
取 )
)
(2)若中間草地的造價為 元
元 ,四個花壇的造價為
,四個花壇的造價為 元
元 ,其余區域的造價為
,其余區域的造價為 元
元 ,當
,當 取何值時,可使“環島”的整體造價最低?
取何值時,可使“環島”的整體造價最低? ,
, (其中
(其中 為常數);
為常數);
(Ⅰ)如果函數 和
和 有相同的極值點,求
有相同的極值點,求 的值;
的值;
(Ⅱ)設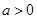 ,問是否存在
,問是否存在 ,使得
,使得 ,若存在,請求出實數
,若存在,請求出實數 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
(Ⅲ)記函數 ,若函數
,若函數 有5個不同的零點,求實數
有5個不同的零點,求實數 的取值范圍.
的取值范圍.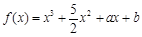 (
( 為常數),其圖象是曲線
為常數),其圖象是曲線 .
.
(1)當 時,求函數
時,求函數 的單調減區間;
的單調減區間;
(2)設函數 的導函數為
的導函數為 ,若存在唯一的實數
,若存在唯一的實數 ,使得
,使得 與
與 同時成立,求實數
同時成立,求實數 的取值范圍;
的取值范圍;
(3)已知點 為曲線
為曲線 上的動點,在點
上的動點,在點 處作曲線
處作曲線 的切線
的切線 與曲線
與曲線 交于另一點
交于另一點 ,在點
,在點 處作曲線
處作曲線 的切線
的切線 ,設切線
,設切線 的斜率分別為
的斜率分別為 .問:是否存在常數
.問:是否存在常數 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.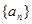 的前n項和為Sn,對一切正整數n,點
的前n項和為Sn,對一切正整數n,點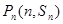 在函數
在函數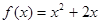 的圖像上,且過點
的圖像上,且過點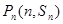 的切線的斜率為kn.
的切線的斜率為kn.
(1)求數列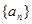 的通項公式;
的通項公式;
(2)若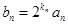 ,求數列
,求數列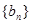 的前n項和Tn.
的前n項和Tn. ,設
,設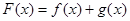
(Ⅰ)求函數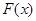 的單調區間
的單調區間
(Ⅱ)若以函數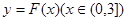 圖象上任意一點
圖象上任意一點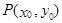 為切點的切線的斜率
為切點的切線的斜率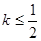 恒成立,求實數
恒成立,求實數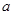 的最小值
的最小值
(Ⅲ)是否存在實數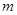 ,使得函數
,使得函數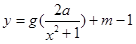 的圖象與函數
的圖象與函數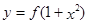 的圖象恰有四個不同交點?若存在,求出實數
的圖象恰有四個不同交點?若存在,求出實數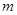 的取值范圍;若不存在,說明理由。
的取值范圍;若不存在,說明理由。
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號