
(本小題滿分12分)
數列 的前
的前 項和為
項和為 ,若
,若 ,點
,點 在直線
在直線 上.
上.
⑴求證:數列 是等差數列;
是等差數列;
⑵若數列 滿足
滿足 ,求數列
,求數列 的前
的前 項和
項和 ;
;
⑶設 ,求證:
,求證: .
.
(1)根據點 在直線
在直線
 上,那么得到
上,那么得到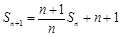 ,兩邊同時除以n得到結論。
,兩邊同時除以n得到結論。
(2) (3)根據
(3)根據 ,利用分組求和法來求解數列的和式,進而放縮得到結論。
,利用分組求和法來求解數列的和式,進而放縮得到結論。
解析試題分析:)⑴∵點 在直線
在直線
 上,
上,
∴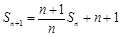 .
.
兩邊同除以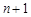 ,得
,得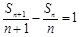 ,
,
于是 是以
是以 為首項,
為首項,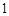 為公差的等差數列.………………..4分
為公差的等差數列.………………..4分
⑵由⑴可知, ,即
,即 ,
,
∴當 時,
時, ,
,
當 時,
時,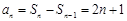 ,
,
經檢驗,當 時也成立,∴
時也成立,∴ .
.
于是 .
.
∵ ,
,
∴ ,
,
相減,解得: .……………………8分
.……………………8分
⑶∵ ,
,
∴

 .………………….12分
.………………….12分
考點:本試題考查了等差數列和等比數列的概念,以及數列求和。
點評:解決該試題的關鍵是對于等差數列和等比數列的通項公式的熟練表示和求解,注意對于已知和式求解通項公式的時候,要注意對于首項的驗證,這個是易錯點。同時要掌握錯位相減法求和,屬于中檔題。


科目:高中數學 來源: 題型:解答題
已知數列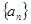 中,
中, 且點
且點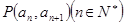 在直線
在直線 上。
上。
(1)求數列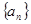 的通項公式;
的通項公式; (2)
(2)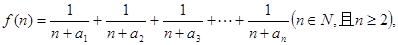 求函數
求函數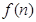 的最小值;
的最小值;
(3)設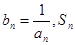 表示數列
表示數列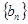 的前
的前 項和。試問:是否存在關于
項和。試問:是否存在關于 的整式
的整式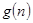 ,使得
,使得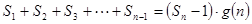 對于一切不小于2的自然數
對于一切不小于2的自然數 恒成立?若存在,寫出
恒成立?若存在,寫出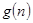 的解析式,并加以證明;若不存在,試說明理由。
的解析式,并加以證明;若不存在,試說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知數列 滿足
滿足 ,數列
,數列 滿足
滿足 ,
,
數列 滿足
滿足 .
.
(1)若 ,證明數列
,證明數列 為等比數列;
為等比數列;
(2)在(1)的條件下,求數列 的通項公式;
的通項公式;
(3)若 ,證明數列
,證明數列 的前
的前 項和
項和 滿足
滿足 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(13分)已知數列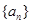 是公差為正的等差數列,其前
是公差為正的等差數列,其前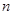 項和為
項和為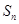 ,點
,點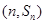 在拋物線
在拋物線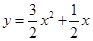 上;各項都為正數的等比數列
上;各項都為正數的等比數列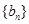 滿足
滿足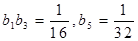 .
.
(1)求數列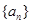 ,
,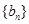 的通項公式;
的通項公式;
(2)記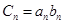 ,求數列
,求數列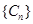 的前n項和
的前n項和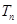 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com