
已知函數(shù)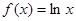
(Ⅰ)若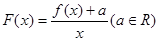 ,求
,求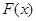 的極大值;
的極大值;
(Ⅱ)若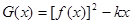 在定義域內(nèi)單調(diào)遞減,求滿足此條件的實(shí)數(shù)k的取值范圍.
在定義域內(nèi)單調(diào)遞減,求滿足此條件的實(shí)數(shù)k的取值范圍.
(Ⅰ)F(x)取得極大值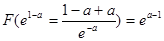 .(Ⅱ)
.(Ⅱ)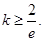
解析試題分析:(Ⅰ)利用“求導(dǎo)數(shù),求駐點(diǎn),討論駐點(diǎn)左右區(qū)間的單調(diào)性,求極值”.
(Ⅱ)由G (x)在定義域內(nèi)單調(diào)遞減知: 在(0+∞)內(nèi)恒成立.
在(0+∞)內(nèi)恒成立.
通過構(gòu)造函數(shù)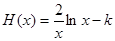 ,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,確定H(x)取最大值
,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,確定H(x)取最大值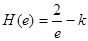
由 恒成立,確定得到實(shí)數(shù)k的取值范圍.
恒成立,確定得到實(shí)數(shù)k的取值范圍.
試題解析:(Ⅰ) 定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/52/b/1duho3.png" style="vertical-align:middle;" />
定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/52/b/1duho3.png" style="vertical-align:middle;" />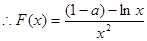 2分
2分
令 由
由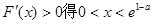
由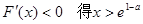 4分
4分
即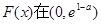 上單調(diào)遞增,在
上單調(diào)遞增,在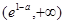 上單調(diào)遞減
上單調(diào)遞減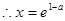 時(shí),F(xiàn)(x)取得極大值
時(shí),F(xiàn)(x)取得極大值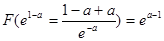 6分
6分
(Ⅱ)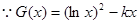 的定義域?yàn)?0+∞)
的定義域?yàn)?0+∞) 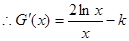
由G (x)在定義域內(nèi)單調(diào)遞減知: 在(0+∞)內(nèi)恒成立 8分
在(0+∞)內(nèi)恒成立 8分
令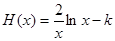 ,則
,則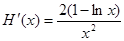 由
由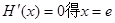
∵當(dāng)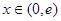 時(shí)
時(shí) 為增函數(shù)
為增函數(shù)
當(dāng) 時(shí)
時(shí)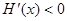
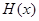 為減函數(shù) 10分
為減函數(shù) 10分
∴當(dāng)x = e時(shí),H(x)取最大值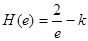
故只需 恒成立,
恒成立,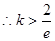
又當(dāng) 時(shí),只有一點(diǎn)x = e使得
時(shí),只有一點(diǎn)x = e使得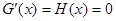 不影響其單調(diào)性
不影響其單調(diào)性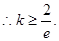 12分
12分
考點(diǎn):利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、極值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)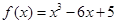 ,
,
(Ⅰ)求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)求函數(shù) 在區(qū)間
在區(qū)間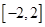 上的最值.
上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)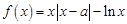 ,
,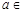
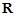 .
.
(Ⅰ)若 ,求函數(shù)
,求函數(shù)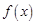 在區(qū)間
在區(qū)間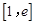 上的最值;
上的最值;
(Ⅱ)若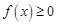 恒成立,求
恒成立,求 的取值范圍. (注:
的取值范圍. (注: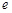 是自然對(duì)數(shù)的底數(shù))
是自然對(duì)數(shù)的底數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(Ⅰ)當(dāng) 時(shí),求
時(shí),求 的極值;
的極值;
(Ⅱ)若 在區(qū)間
在區(qū)間 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù)h(x)=ax2+bx+c(其中c<3),其導(dǎo)函數(shù) 的圖象如圖,f(x)=6lnx+h(x).
的圖象如圖,f(x)=6lnx+h(x).
①求f(x)在x=3處的切線斜率;
②若f(x)在區(qū)間(m,m+ )上是單調(diào)函數(shù),求實(shí)數(shù)m的取值范圍;
)上是單調(diào)函數(shù),求實(shí)數(shù)m的取值范圍;
③若對(duì)任意k∈[-1,1],函數(shù)y=kx(x∈(0,6])的圖象總在函數(shù)y=f(x)圖象的上方,求c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)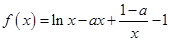 .
.
(1)當(dāng)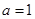 時(shí),求曲線
時(shí),求曲線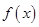 在
在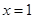 處的切線方程;
處的切線方程;
(2)當(dāng)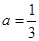 時(shí),求函數(shù)
時(shí),求函數(shù)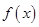 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)在(2)的條件下,設(shè)函數(shù)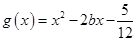 ,若對(duì)于
,若對(duì)于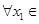 [1,2],
[1,2],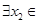 [0,1],使
[0,1],使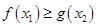 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) 在
在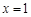 處取得極值.
處取得極值.
(1)求實(shí)數(shù) 的值;
的值;
(2)若關(guān)于 的方程
的方程 在
在 上恰有兩個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù)
上恰有兩個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù) 的取值范圍;
的取值范圍;
(3)若
 ,使
,使 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 (
( ).
).
(1)當(dāng) 時(shí),判斷
時(shí),判斷 在定義域上的單調(diào)性;
在定義域上的單調(diào)性;
(2)若 在
在 上的最小值為
上的最小值為 ,求
,求 的值;
的值;
(3)若 在
在 上恒成立,試求
上恒成立,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,它的一個(gè)極值點(diǎn)是
,它的一個(gè)極值點(diǎn)是 .
.
(Ⅰ) 求 的值及
的值及 的值域;
的值域;
(Ⅱ)設(shè)函數(shù) ,試求函數(shù)
,試求函數(shù) 的零點(diǎn)的個(gè)數(shù).
的零點(diǎn)的個(gè)數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com