
某校夏令營有3名男同學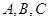 和3名女同學
和3名女同學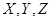 ,其年級情況如下表:
,其年級情況如下表:
| | 一年級 | 二年級 | 三年級 |
| 男同學 |  | 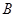 | 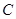 |
| 女同學 | 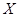 | 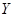 | 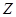 |
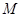 為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件
為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件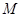 發生的概率.
發生的概率. (1)見解析(2)
解析試題分析:(1)利用列舉法將從三個年級A、B、C、X、Y、Z六名同學中任選人的所有可能結果列出來即可;(2)找出上述結果中,選出的2人來自不同年級且恰有1名男同學和1名女同學的所有可能結果,根據古典概型公式即可求出概率.
試題解析: (1)從6名同學中隨機選出2人參加知識競賽的所有可能結果為{A,B},{A,C},{A,X},{A,Y},{A,Z},{B,C},{B,X},{B,Y},{B,Z},{C,X},{C,Y},{C,Z},{X,Y},{X,Z},{Y,Z},共15種.
(2)選出的2人來自不同年級且恰有1名男同學和1名女同學的所有可能結果為{A,Y},{A,Z},{B,X},{B,Z},{C,X},{C,Y},共6種.
因此,事件M發生的概率P(M)=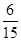 =
= .
.
考點:古典概型


科目:高中數學 來源: 題型:填空題
某旅游公司有甲、乙、丙三種特色產品,其數量分別為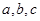 (單位:件),且
(單位:件),且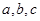 成等差數列。現采用分層抽樣的方法從中抽取30 件,其中已知抽到甲產品的概率為
成等差數列。現采用分層抽樣的方法從中抽取30 件,其中已知抽到甲產品的概率為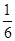 ,則抽到丙產品的件數為 .
,則抽到丙產品的件數為 .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個袋中裝有大小相同的黑球和白球共9個,從中任取2個球,記隨機變量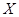 為取出2球中白球的個數,已知
為取出2球中白球的個數,已知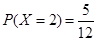 .
.
(Ⅰ)求袋中白球的個數;
(Ⅱ)求隨機變量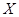 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從天氣網查詢到衡水歷史天氣統計 (2011-01-01到2014-03-01)資料如下: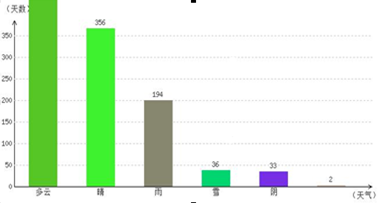
自2011-01-01到2014-03-01,衡水共出現:多云507天,晴356天,雨194天,雪36天,陰33天,其它2天,合計天數為:1128天。
本市朱先生在雨雪天的情況下,分別以 的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據:
的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據: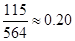 )
)
(1)求他某天打出租上班的概率;
(2)將他每天上班所需的費用記為 (單位:元),求
(單位:元),求 的分布列及數學期望。
的分布列及數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校舉行綜合知識大獎賽,比賽分初賽和決賽兩部分,初賽采用選手選一題答一題的方式進行,每位選手最多有6次答題的機會,選手累計答對4題或答錯3題即終止其初賽的比賽,答對4題者直接進入決賽,答錯3題者則被淘汰.已知選手甲答題連續兩次答錯的概率為 (已知甲回答每道題的正確率相同,并且相互之間沒有影響).
(已知甲回答每道題的正確率相同,并且相互之間沒有影響).
(Ⅰ)求選手甲回答一個問題的正確率;
(Ⅱ)求選手甲可以進入決賽的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲有大小相同的兩張卡片,標有數字2、3;乙有大小相同的卡片四張,分別標有1、2、3、4.
(1)求乙隨機抽取的兩張卡片的數字之和為奇數的概率;
(2)甲、乙分別取出一張卡,比較數字,數字大者獲勝,求乙獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區為了解高二學生作業量和玩電腦游戲的情況,對該地區內所有高二學生采用隨機抽樣的方法,得到一個容量為200的樣本.統計數據如下:
(1)已知該地區共有高二學生42500名,根據該樣本估計總體,其中喜歡電腦游戲并認為作業不多的人有多少名?
(2)在A,B,C,D,E,F六名學生中,僅有A,B兩名學生認為作業多.如果從這六名學生中隨機抽取兩名,求至少有一名學生認為作業多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量a=(2,1),b=(x,y).
(1)若x∈{-1,0,1,2},y∈{-1,0,1},求向量a∥b的概率;
(2)若x∈[-1,2],y∈[-1,1],求向量a,b的夾角是鈍角的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com