
從天氣網查詢到衡水歷史天氣統計 (2011-01-01到2014-03-01)資料如下: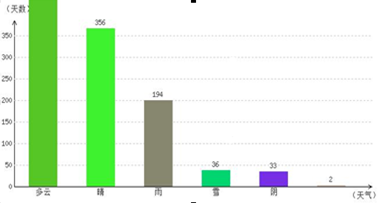
自2011-01-01到2014-03-01,衡水共出現:多云507天,晴356天,雨194天,雪36天,陰33天,其它2天,合計天數為:1128天。
本市朱先生在雨雪天的情況下,分別以 的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據:
的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為2元或40元;在非雨雪天的情況下,他以90%的概率騎自行車上班,每天交通費用0元;另外以10%的概率打出租上班,每天交通費用20元。(以頻率代替概率,保留兩位小數.參考數據: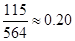 )
)
(1)求他某天打出租上班的概率;
(2)將他每天上班所需的費用記為 (單位:元),求
(單位:元),求 的分布列及數學期望。
的分布列及數學期望。
(1)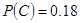 ;
;
(2)
0 2 20 40 
0.72 0.10 0.08 0.10 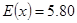
解析試題分析:(1)利用定義,求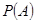 和
和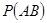 ,則
,則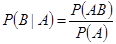 ;(2)借助古典概型概率公式,先求事件
;(2)借助古典概型概率公式,先求事件 包含的基本事件數
包含的基本事件數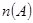 ,再求事件
,再求事件 和事件
和事件 的交事件中包含的基本事件數
的交事件中包含的基本事件數 ,得
,得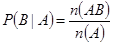 ;(3)求解離散隨機變量分布列和方差,首先要理解問題的關鍵,其次要準確無誤的找出隨機變量的所有可能值,計算出相對應的概率,寫成隨機變量的分布列,正確運用均值、方差公式進行計算.
;(3)求解離散隨機變量分布列和方差,首先要理解問題的關鍵,其次要準確無誤的找出隨機變量的所有可能值,計算出相對應的概率,寫成隨機變量的分布列,正確運用均值、方差公式進行計算.
試題解析:解:(Ⅰ)設 表示事件“雨雪天”,
表示事件“雨雪天”, 表示事件“非雨雪天”,
表示事件“非雨雪天”, 表示事件“打出租上班”,
表示事件“打出租上班”,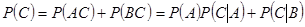 2分
2分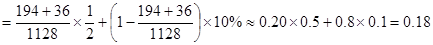 4分
4分
(Ⅱ) 的可能取值為0,2,20,40 6分
的可能取值為0,2,20,40 6分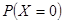
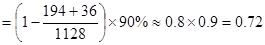
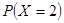
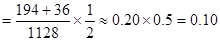
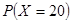
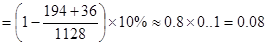
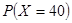
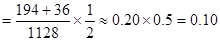 10分
10分
∴ 的分布列為
的分布列為
0 2 20 40 
0.72 0.10 0.08 0.10 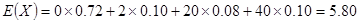 (元) 12分
(元) 12分
考點:(1)條件概率的應用.(2)離散型隨機變量的分布和數學期望.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:填空題
在棱長為2的正方體ABCDA1B1C1D1中,點O為底面ABCD的中心,在正方體ABCD
A1B1C1D1內隨機取一點P,則點P到點O的距離大于1的概率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在乒乓球比賽中,甲與乙以“五局三勝”制進行比賽,根據以往比賽情況,甲在每一局勝乙的概率均為  .已知比賽中,乙先贏了第一局,求:
.已知比賽中,乙先贏了第一局,求:
(Ⅰ)甲在這種情況下取勝的概率;
(Ⅱ)設比賽局數為X,求X的分布列及數學期望(均用分數作答)。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
春節期間,某商場決定從3種服裝、2種家電、3種日用品中,選出3種商品進行促銷活動。
⑴)試求選出的3種商品中至少有一種是家電的概率;
⑵商場對選出的某商品采用抽獎方式進行促銷,即在該商品現價的基礎上將價格提高100元,規定購買該商品的顧客有3次抽獎的機會:若中一次獎,則獲得數額為 元的獎金;若中兩次獎,則共獲得數額為
元的獎金;若中兩次獎,則共獲得數額為 元的獎金;若中3次獎,則共獲得數額為
元的獎金;若中3次獎,則共獲得數額為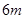 元的獎金。假設顧客每次抽獎中獲的概率都是
元的獎金。假設顧客每次抽獎中獲的概率都是 ,請問:商場將獎金數額m最高定為多少元,才能使促銷方案對商場有利?
,請問:商場將獎金數額m最高定為多少元,才能使促銷方案對商場有利?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校夏令營有3名男同學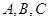 和3名女同學
和3名女同學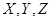 ,其年級情況如下表:
,其年級情況如下表:
| | 一年級 | 二年級 | 三年級 |
| 男同學 |  | 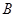 | 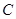 |
| 女同學 | 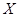 | 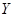 | 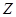 |
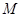 為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件
為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件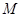 發生的概率.
發生的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下圖是淮北市6月1日至14日的空氣質量指數趨勢圖,空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染.某人隨機選擇6月1日至6月15日中的某一天到達該市,并停留2天.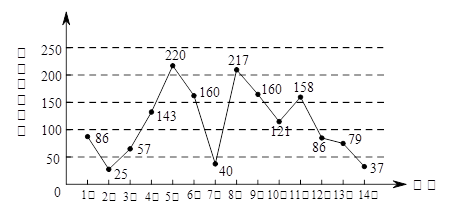
(1)求此人到達當日空氣重度污染的概率;
(2)若設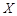 是此人停留期間空氣質量優良的天數,請分別求當x=0時,x=1時和x=3時的概率值。
是此人停留期間空氣質量優良的天數,請分別求當x=0時,x=1時和x=3時的概率值。
(3)由圖判斷從哪天開始淮北市連續三天的空氣質量指數方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
去年2月29日,我國發布了新修訂的《環境空氣質量標準》指出空氣質量指數在 為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為
為優秀,各類人群可正常活動.惠州市環保局對我市2014年進行為期一年的空氣質量監測,得到每天的空氣質量指數,從中隨機抽取50個作為樣本進行分析報告,樣本數據分組區間為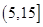 ,
,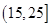 ,
,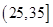 ,
,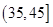 ,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
,由此得到樣本的空氣質量指數頻率分布直方圖,如圖.
(1) 求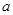 的值;
的值;
(2) 根據樣本數據,試估計這一年度的空氣質量指數的平均值;(注:設樣本數據第 組的頻率為
組的頻率為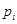 ,第
,第 組區間的中點值為
組區間的中點值為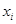
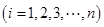 ,則樣本數據的平均值為
,則樣本數據的平均值為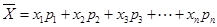 .)
.)
(3) 如果空氣質量指數不超過 ,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取
,就認定空氣質量為“特優等級”,則從這一年的監測數據中隨機抽取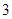 天的數值,其中達到“特優等級”的天數為
天的數值,其中達到“特優等級”的天數為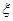 ,求
,求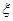 的分布列和數學期望.
的分布列和數學期望.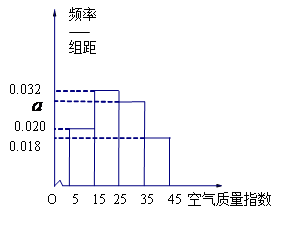
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
哈六中體育節進行定點投籃游戲,已知參加游戲的甲、乙兩人,他們每一次投籃投中的概率均為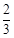 ,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.(12分)
,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.(12分)
(1)求甲同學至少有4次投中的概率;
(2)求乙同學投籃次數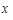 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com