
(本題滿分12分)
已知橢圓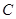 的兩焦點是
的兩焦點是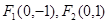 ,離心率
,離心率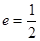 .
.
(Ⅰ)求橢圓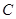 的方程;
的方程;
(Ⅱ)若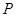 在橢圓
在橢圓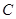 上,且
上,且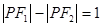 ,求DPF1F2的面積.
,求DPF1F2的面積.
 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知橢圓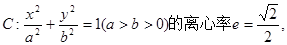 左、右焦點分別為F1、F2,點
左、右焦點分別為F1、F2,點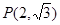 ,點F2在線段PF1的中垂線上。
,點F2在線段PF1的中垂線上。
(1)求橢圓C的方程;
(2)設直線 與橢圓C交于M、N兩點,直線F2M與F2N的傾斜角互補,求證:直線
與橢圓C交于M、N兩點,直線F2M與F2N的傾斜角互補,求證:直線 過定點,并求該定點的坐標。
過定點,并求該定點的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知橢圓M的中心為坐標原點,且焦點在x軸上,若M的一個頂點恰好是拋物線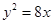 的焦點,M的離心率
的焦點,M的離心率 ,過M的右焦點F作不與坐標軸垂直的直線
,過M的右焦點F作不與坐標軸垂直的直線 ,交M于A,B兩點。
,交M于A,B兩點。
(1)求橢圓M的標準方程;
(2)設點N(t,0)是一個動點,且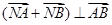 ,求實數t的取值范圍。
,求實數t的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本大題滿分14分)
已知△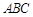 的兩個頂點
的兩個頂點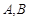 的坐標分別是
的坐標分別是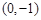 ,
,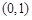 ,且
,且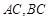 所在直線的斜率之積等于
所在直線的斜率之積等于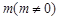 .
.
(Ⅰ)求頂點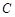 的軌跡
的軌跡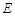 的方程,并判斷軌跡
的方程,并判斷軌跡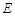 為何種圓錐曲線;
為何種圓錐曲線;
(Ⅱ)當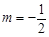 時,過點
時,過點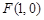 的直線
的直線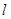 交曲線
交曲線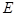 于
于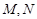 兩點,設點
兩點,設點 關于
關于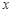 軸的對稱點為
軸的對稱點為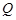 (
(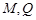 不重合).求證直線
不重合).求證直線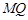 與
與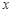 軸的交點為定點,并求出該定點的坐標.
軸的交點為定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知兩點F1(-1,0)及F2(1,0),點P在以F1、F2為焦點的橢圓C上,且|PF1|、|F1F2|、|PF2|構成等差數列.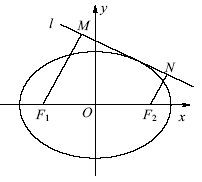
(1)求橢圓C的方程;
(2)如圖,動直線l:y=kx+m與橢圓C有且僅有一個公共點,點M,N是直線l上的兩點,且F1M⊥l,F2N⊥l.求四邊形F1MNF2面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 、
、 分別是橢圓
分別是橢圓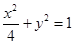 的左、右焦點。
的左、右焦點。
(1)若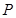 是第一象限內該橢圓上的一點,
是第一象限內該橢圓上的一點,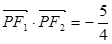 ,求點P的坐標;
,求點P的坐標;
(2)設過定點M(0,2)的直線 與橢圓交于不同的兩點A、B,且
與橢圓交于不同的兩點A、B,且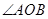 為銳角(其中
為銳角(其中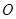 為坐標原點),求直線
為坐標原點),求直線 的斜率
的斜率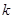 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com