
已知函數 .
.
(1)討論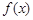 的單調性;
的單調性;
(2)設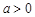 ,證明:當
,證明:當 時,
時,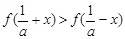 ;
;
(3)若函數 的圖像與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明:
的圖像與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明: (x0)<0.(本題滿分14分)
(x0)<0.(本題滿分14分)
(1)若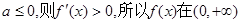 單調增加.
單調增加.
若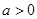 ,
,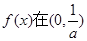 單調增加,在
單調增加,在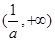 單調減少.
單調減少.
(2)見解析。
解析試題分析:解:(1)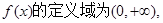 …………………………………………1分
…………………………………………1分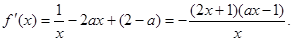 …………………………2分
…………………………2分
(i)若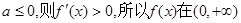 單調增加.…………………3分
單調增加.…………………3分
(ii)若
且當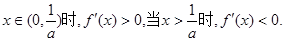
所以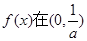 單調增加,在
單調增加,在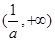 單調減少. ……………………5分
單調減少. ……………………5分
(2)設函數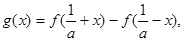 則
則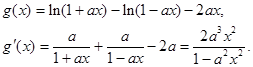
…………………………………7分
當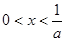 時,
時,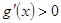 ,所以
,所以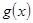 單調遞增,
單調遞增,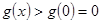
故當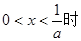 ,
,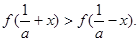 ……………………………9分
……………………………9分
(3)由(I)可得,當 的圖像與x軸至多有一個交點,
的圖像與x軸至多有一個交點,
故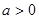 ,從而
,從而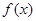 的最大值為
的最大值為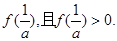
不妨設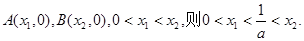
由(II)得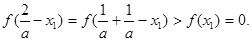
從而
由(I)知,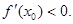 …………………………………………………14分
…………………………………………………14分
考點:本題考查利用導數求函數的單調性、綜合分析和解決問題的能力以及分類討論的思想方法。
點評:解答本題易出現以下失誤:①忘記求函數的定義域;②想不到分類討論,從而在判斷函數的單調性時出現錯誤。當求函數的單調性時,如果無法判斷導函數的符號,自然而然的就應該想到分類討論,為了避免錯誤的發生,在平常做題時就要養成分析思路的習慣。


科目:高中數學 來源: 題型:解答題
(本題滿分12分)
一列火車在平直的鐵軌上行駛,由于遇到緊急情況,火車以速度 (單位:m/s)緊急剎車至停止。求:
(單位:m/s)緊急剎車至停止。求:
(I)從開始緊急剎車到火車完全停止所經過的時間;
(Ⅱ)緊急剎車后火車運行的路程。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
本題滿分15分)已知函數 ,
, .
.
(Ⅰ)當 時,求函數
時,求函數 的極值點;
的極值點;
(Ⅱ)若函數 在導函數
在導函數 的單調區間上也是單調的,求
的單調區間上也是單調的,求 的取值范圍;
的取值范圍;
(Ⅲ) 當 時,設
時,設 ,且
,且 是函數
是函數 的極值點,證明:
的極值點,證明: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)
已知函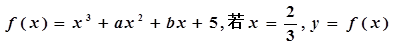 有極值,且曲線
有極值,且曲線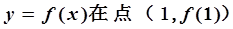 處的切線斜率為3.
處的切線斜率為3.
(1)求函數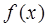 的解析式;
的解析式;
(2)求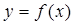 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函數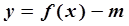 有三個零點,求實數
有三個零點,求實數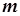 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com