
已知函數 ,
,
(1)若 ,求函數的零點;
,求函數的零點;
(2)若函數在區間 上恰有一個零點,求
上恰有一個零點,求 的取值范圍.
的取值范圍.
(1)1;(2)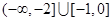 .
.
解析試題分析:(1) 代入,求
代入,求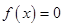 可得零點; (2)函數在區間上恰有一個零點,轉化為一元二次方程根的在
可得零點; (2)函數在區間上恰有一個零點,轉化為一元二次方程根的在 只有一個解,可得關于
只有一個解,可得關于 的關系式,進一步求得
的關系式,進一步求得 的范圍.
的范圍.
試題解析:
解:(1)若 ,則
,則 , 1分
, 1分
由 =0,
=0,
得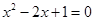 , 2分
, 2分
解得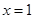 , 4分
, 4分
∴當 時,函數
時,函數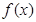 的零點是1. 5分
的零點是1. 5分
(2)已知函數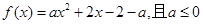
①當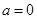 時,
時,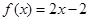 ,由
,由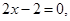 得
得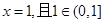 ,
,
∴當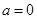 時,函數
時,函數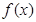 在區間
在區間 上恰有一個零點. 6分
上恰有一個零點. 6分
當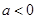 時,
時, 7分
7分
②若 ,則
,則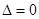 ,由(1)知函數
,由(1)知函數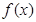 的零點是
的零點是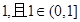 ,
,
∴當 時,函數
時,函數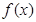 在區間
在區間 上恰有一個零點. 8分
上恰有一個零點. 8分
③若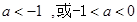 ,則
,則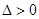 ,
,
由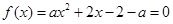 ,
,
解得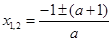 ,即
,即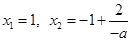 , 10分
, 10分
∴函數 在區間
在區間 上必有一個零點
上必有一個零點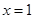 .
.
要使函數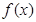 在區間
在區間 上恰有一個零點.
上恰有一個零點.
必須 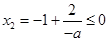 ,或
,或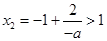 , 11分
, 11分
解得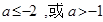 , 13分
, 13分
又∵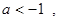 或
或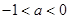 ,
,
∴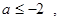 或
或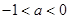 ,
,
綜合①②③得, 的取值范圍是
的取值范圍是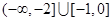 . 14分
. 14分
考點:函數的零點,一元二次方程根的分布.


科目:高中數學 來源: 題型:解答題
設f(x)是(-∞,+∞)上的奇函數,f(x+2)=-f(x),
當0≤x≤1時,f(x)=x.
(1)求f(3)的值;
(2)當-4≤x≤4時,求f(x)的圖像與x軸所圍成圖形的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某幼兒園準備建一個轉盤,轉盤的外圍是一個周長為k米的圓.在這個圓上安裝座位,且每個座位和圓心處的支點都有一根直的鋼管相連經預算,轉盤上的每個座位與支點相連的鋼管的費用為3k元/根,且當兩相鄰的座位之間的圓弧長為x米時,相鄰兩座位之間的鋼管和其中一個座位的總費用為 k元.假設座位等距分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記轉盤的總造價為y元.
k元.假設座位等距分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記轉盤的總造價為y元.
(1)試寫出y關于x的函數關系式,并寫出定義域;
(2)當k=50米時,試確定座位的個數,使得總造價最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com