
對于定義在實數集 上的兩個函數
上的兩個函數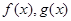 ,若存在一次函數
,若存在一次函數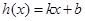 使得,對任意的
使得,對任意的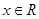 ,都有
,都有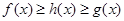 ,則把函數
,則把函數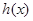 的圖像叫函數
的圖像叫函數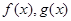 的“分界線”。現已知
的“分界線”。現已知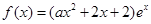 (
(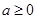 ,
,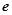 為自然對數的底數),
為自然對數的底數),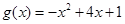
(1)求 的遞增區間;
的遞增區間;
(2)當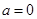 時,函數
時,函數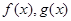 是否存在過點
是否存在過點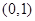 的“分界線”?若存在,求出函數
的“分界線”?若存在,求出函數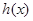 的解析式,若不存在,請說明理由。
的解析式,若不存在,請說明理由。
(1)若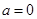 遞增區間為
遞增區間為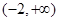 ,若
,若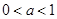 遞增區間為
遞增區間為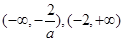 ,若
,若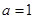 ,則遞增區間為
,則遞增區間為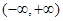 若
若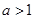 遞增區間為
遞增區間為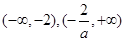 (2)存在函數
(2)存在函數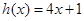 的圖像是函數
的圖像是函數 過點
過點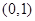 的“分界線”。
的“分界線”。
解析試題分析:(1)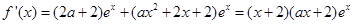 ,
,
由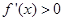 得
得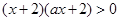
①若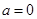 ,則
,則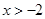 ,此時
,此時 的遞增區間為
的遞增區間為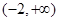 ;
;
②若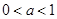 ,則
,則 或
或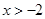 ,此時
,此時 的遞增區間為
的遞增區間為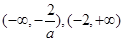 ;
;
③若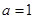 ,則
,則 的遞增區間為
的遞增區間為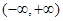 ;
;
④若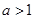 ,則
,則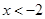 或
或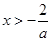 ,此時
,此時 的遞增區間為
的遞增區間為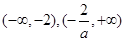 。
。
(2)當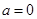 時,
時,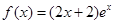 ,假設存在實數
,假設存在實數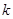 ,使不等式
,使不等式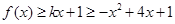 對
對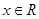 恒成立,
恒成立,
由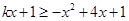 得到
得到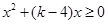 對
對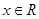 恒成立,
恒成立,
則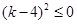 ,得
,得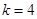 ,
,
下面證明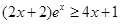 對
對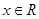 恒成立。
恒成立。
設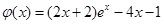 ,
,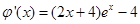 ,
,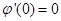 ,
,
且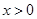 時,
時,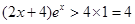 ,
,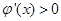 ,
,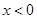 時,
時,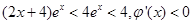 ,
,
所以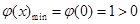 ,即
,即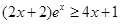 對
對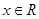 恒成立。
恒成立。
綜上,存在函數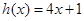 的圖像是函數
的圖像是函數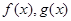 過點
過點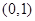 的“分界線”。
的“分界線”。
考點:函數單調區間及不等式恒成立
點評:第一小題求單調區間針對于不同的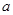 值對應不同的極值點,因此需對
值對應不同的極值點,因此需對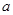 值分情況討論以求單調性;第二問在正確理解給定信息的基礎上將問題轉化為不等式恒成立問題,進而轉化為函數最值,可利用導數這一工具求解
值分情況討論以求單調性;第二問在正確理解給定信息的基礎上將問題轉化為不等式恒成立問題,進而轉化為函數最值,可利用導數這一工具求解


科目:高中數學 來源: 題型:解答題
如圖,已知正比例函數y=2x的圖像l1與反比例函數y= 的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
(1)求反比例函數的解析式;
(2)求△DOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com