
(本小題滿分12分)已知函數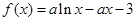 (a∈R且
(a∈R且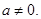 ).
).
(1)求函數f(x)的單調區間;
(2)若函數y=f(x)的圖象在點(2,f(2))處的切線的傾斜角為45°,對于任意t∈[1,2],函數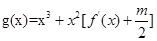 在區間(t,3)上總不是單調函數,求m的取值范圍.
在區間(t,3)上總不是單調函數,求m的取值范圍.
(1) 當a>0時,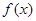 的單調增區間為(0,1),單調減區間為(1,+∞)
的單調增區間為(0,1),單調減區間為(1,+∞)
當a<0時,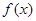 的單調增區間為(1,+∞),單調減區間為(0,1)
的單調增區間為(1,+∞),單調減區間為(0,1)
(2)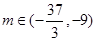
解析試題分析:解:(本小題滿分12分)
(1)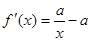 =
=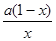 . ∵x>0, ………………………1分
. ∵x>0, ………………………1分
當a>0時,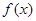 的單調增區間為(0,1),單調減區間為(1,+∞)……………2分
的單調增區間為(0,1),單調減區間為(1,+∞)……………2分
當a<0時,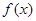 的單調增區間為(1,+∞),單調減區間為(0,1).……………4分
的單調增區間為(1,+∞),單調減區間為(0,1).……………4分
(2)∵函數y=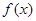 在點(2,
在點(2,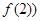 處的切線斜率為1,
處的切線斜率為1,
∴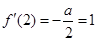 , 解得a=-2.………………………………5分
, 解得a=-2.………………………………5分
∴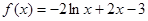 , ∴
, ∴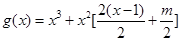
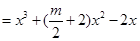 .
.
∴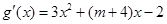 .……………………………7分
.……………………………7分
令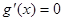 ,即
,即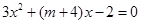 , ∵△=
, ∵△=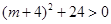 ,
,
∴方程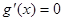 有兩個實根且兩根一正一負,即有且只有一個正根.…………8分
有兩個實根且兩根一正一負,即有且只有一個正根.…………8分
∵函數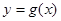 在區間(t,3)(其中t∈[1,2])上總不是單調函數,
在區間(t,3)(其中t∈[1,2])上總不是單調函數,
∴方程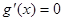 在
在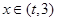 上有且只有一個實數根.………………………9分
上有且只有一個實數根.………………………9分
又∵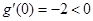 ,∴
,∴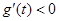 ,
,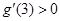 .
.
∴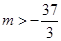 ,且
,且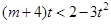 .…………………………………………10分
.…………………………………………10分
∵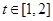 ,∴
,∴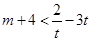 ,
,
令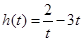 ,則
,則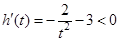 ,即
,即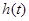 在
在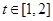 上單調遞減.
上單調遞減.
∴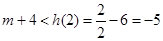 ,即
,即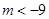 .
.
∴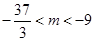 .
.
綜上可得,m的取值范圍為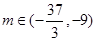 .…………………………………12分
.…………………………………12分
考點:本試題考查了導數的運用
點評:解決該試題的關鍵是能理解對于導數的符號,運用分類討論的思想來求解函數的單調性。同時對于函數不單調的處理,可以轉換為函數單調時的參數的范圍,然后利用補集的思想求解結論,屬于中檔題。


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知函數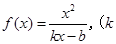 ,
,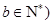 ,滿足
,滿足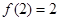 ,
,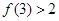 .
.
(1)求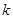 ,
,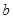 的值;
的值;
(2)若各項為正的數列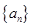 的前
的前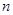 項和為
項和為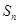 ,且有
,且有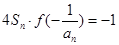 ,設
,設 ,求數列
,求數列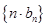 的前
的前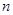 項和
項和 ;
;
(3)在(2)的條件下,證明: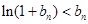 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數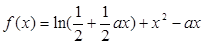
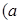 為常數,
為常數,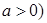
(1)當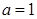 時,求函數
時,求函數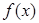 在
在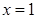 處的切線方程;
處的切線方程;
(2)當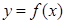 在
在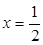 處取得極值時,若關于
處取得極值時,若關于 的方程
的方程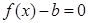 在
在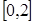 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數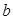 的取值范圍;
的取值范圍;
(3)若對任意的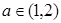 ,總存在
,總存在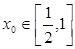 ,使不等式
,使不等式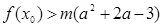 成立,求實數
成立,求實數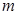 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某種產品投放市場以來,通過市場調查,銷量t(單位:噸)與利潤Q(單位:萬元)的變化關系如右表,現給出三種函數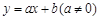 ,
,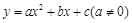 ,
,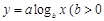 且
且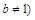 ,請你根據表中的數據,選取一個恰當的函數,使它能合理描述產品利潤Q與銷量t的變化,求所選取的函數的解析式,并求利潤最大時的銷量.
,請你根據表中的數據,選取一個恰當的函數,使它能合理描述產品利潤Q與銷量t的變化,求所選取的函數的解析式,并求利潤最大時的銷量.
| 銷量t | 1 | 4 | 6 |
| 利潤Q | 2 | 5 | 4.5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com