
已知f(x)是定義在(0,+∞) 上的非負可導函數,且滿足xf′(x)+f(x)≤0,對任意的0<a<b,則必有( ).
A.af(b)≤bf(a) B.bf(a)≤af(b)
C.af(a)≤f(b) D.bf(b)≤f(a)
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練優化重組卷3練習卷(解析版) 題型:選擇題
設{an}是公差不為0的等差數列,a1=2且a1,a3,a6成等比數列,則{an} 的前n項和Sn=( ).
A. B.
B. C.
C. D.n2+n
D.n2+n
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練x4-1練習卷(解析版) 題型:填空題
如圖,已知Rt△ABC的兩條直角邊AC,BC的長分別為3 cm,4 cm,以AC為直徑的圓與AB交于點D,則BD=________cm.

查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練6練習卷(解析版) 題型:選擇題
已知函數f(x)=sin (2x+φ),其中φ為實數,若f(x)≤ 對x∈R恒成立,且
對x∈R恒成立,且 <f(π),則下列結論正確的是( ).
<f(π),則下列結論正確的是( ).
A. =-1
=-1
B.f >f
>f
C.f(x)是奇函數
D.f(x)的單調遞增區間是 (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練5練習卷(解析版) 題型:解答題
設函數f(x)=ax-(1+a2)x2,其中a>0,區間I={x|f(x)>0}.
(1)求I的長度(注:區間(α,β)的長度定義為β-α);
(2)給定常數k∈(0,1),當1-k≤a≤1+k時,求I長度的最小值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練4練習卷(解析版) 題型:解答題
已知函數f(x)=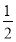 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲線y=f(x)在x=1和x=3處的切線互相平行,求a的值;
(2)求f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練4練習卷(解析版) 題型:選擇題
已知函數y=f(x)(x∈R)的圖象如圖所示,則不等式xf′(x)<0的解集為( ).

A.  ∪
∪ B.
B. 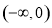 ∪
∪
C.  ∪
∪ D.
D. 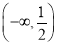 ∪
∪
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練2練習卷(解析版) 題型:填空題
我們把形如y= (a>0,b>0)的函數因其圖象類似于漢字中的“囧”字,故生動地稱為“囧函數”,若當a=1,b=1時的“囧函數”與函數y=lg|x|的交點個數為n,則n=________.
(a>0,b>0)的函數因其圖象類似于漢字中的“囧”字,故生動地稱為“囧函數”,若當a=1,b=1時的“囧函數”與函數y=lg|x|的交點個數為n,則n=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習6-1直線與圓練習卷(解析版) 題型:填空題
在平面直角坐標系xOy中,圓C的方程為x2+y2-8x+15=0,若直線y=kx-2上至少存在一點,使得以該點為圓心,1為半徑的圓與圓C有公共點,則k的最大值是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com