
已知圓錐曲線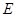 的兩個焦點坐標是
的兩個焦點坐標是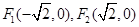 ,且離心率為
,且離心率為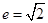 ;
;
(Ⅰ)求曲線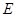 的方程;
的方程;
(Ⅱ)設曲線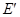 表示曲線
表示曲線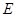 的
的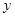 軸左邊部分,若直線
軸左邊部分,若直線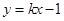 與曲線
與曲線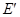 相交于
相交于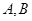 兩點,求
兩點,求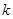 的取值范圍;
的取值范圍;
(Ⅲ)在條件(Ⅱ)下,如果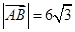 ,且曲線
,且曲線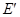 上存在點
上存在點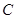 ,使
,使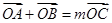 ,求
,求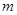 的值.
的值.
(Ⅰ)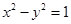 ;(Ⅱ)
;(Ⅱ)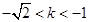 ;(Ⅲ)
;(Ⅲ)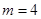 .
.
解析試題分析:(Ⅰ)由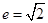 知圓錐曲線
知圓錐曲線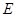 為雙曲線,再由焦點坐標知
為雙曲線,再由焦點坐標知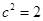 ,從而得
,從而得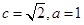 ,即雙曲線
,即雙曲線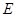 的方程是
的方程是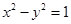 ;(Ⅱ)設出
;(Ⅱ)設出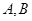 兩點的坐標,再將直線
兩點的坐標,再將直線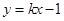 與曲線
與曲線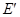 方程聯立,知方程應有兩個根.再由二次項的系數、根的判別式、以及這兩根應為負根,即兩根之和小于0,兩根之積大于0.從而得到
方程聯立,知方程應有兩個根.再由二次項的系數、根的判別式、以及這兩根應為負根,即兩根之和小于0,兩根之積大于0.從而得到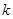 的取值范圍;(Ⅲ)由
的取值范圍;(Ⅲ)由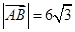 結合上問
結合上問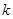 的取值范圍從而得到
的取值范圍從而得到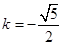 ,然后由
,然后由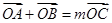 通過向量的坐標表示得到點
通過向量的坐標表示得到點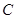 ,代入曲線
,代入曲線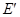 的方程即可.
的方程即可.
試題解析:(Ⅰ)由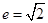 知,曲線
知,曲線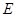 是以
是以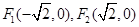 為焦點的雙曲線,且
為焦點的雙曲線,且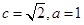 ,
,
故雙曲線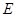 的方程是
的方程是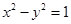 . (3分)
. (3分)
(Ⅱ)設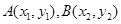 ,聯立方程組:
,聯立方程組: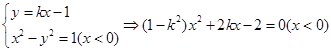 ,
,
從而有: 為所求. (8分)
為所求. (8分)
(Ⅲ)因為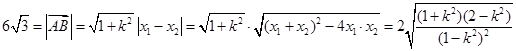 ,
,
整理得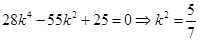 或
或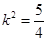 ,
,
注意到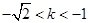 ,所以
,所以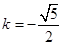 ,故直線
,故直線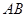 的方程為
的方程為 . (10分)
. (10分)
設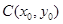 ,由已知
,由已知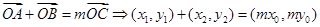 ,
,
又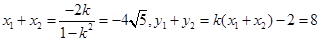 ,所以
,所以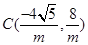 .
.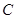 在曲線
在曲線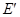 上,得
上,得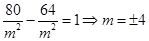 ,
,
但當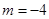 時,所得的點在雙曲線的右支上,不合題意,
時,所得的點在雙曲線的右支上,不合題意,
所以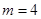 為所求. (13分)
為所求. (13分)
考點:1.雙曲線的幾何性質;2.一元二次方程根的分布;3.直線與圓錐曲線的位置關系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
已知橢圓 (a>b>0)的離心率為
(a>b>0)的離心率為 ,右焦點為(
,右焦點為( ,0).
,0).
(I)求橢圓的方程;
(Ⅱ)過橢圓的右焦點且斜率為k的直線與橢圓交于點A(xl,y1),B(x2,y2),若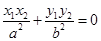 , 求斜率k是的值.
, 求斜率k是的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓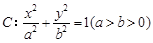 的離心率為
的離心率為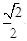 ,其中左焦點
,其中左焦點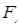 (-2,0).
(-2,0).
(1) 求橢圓C的方程;
(2) 若直線y=x+m與橢圓C交于不同的兩點A,B,且線段AB的中點M在圓x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校同學設計一個如圖所示的“蝴蝶形圖案(陰影區域)”,其中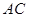 、
、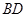 是過拋物線
是過拋物線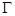 焦點
焦點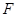 的兩條弦,且其焦點
的兩條弦,且其焦點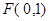 ,
,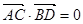 ,點
,點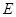 為
為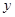 軸上一點,記
軸上一點,記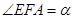 ,其中
,其中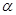 為銳角.
為銳角.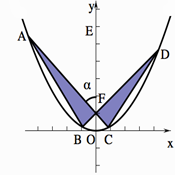
(1)求拋物線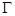 方程;
方程;
(2)求證: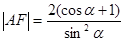 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知拋物線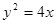 的焦點為F,過F的直線交拋物線于M、N兩點,其準線
的焦點為F,過F的直線交拋物線于M、N兩點,其準線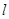 與x軸交于K點.
與x軸交于K點.
(1)求證:KF平分∠MKN;
(2)O為坐標原點,直線MO、NO分別交準線于點P、Q,求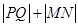 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,過點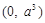 的兩直線與拋物線
的兩直線與拋物線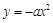 相切于A、B兩點, AD、BC垂直于直線
相切于A、B兩點, AD、BC垂直于直線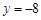 ,垂足分別為D、C.
,垂足分別為D、C.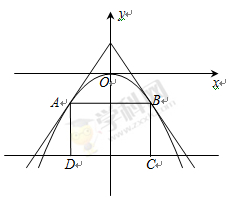
(1)若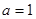 ,求矩形ABCD面積;
,求矩形ABCD面積;
(2)若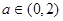 ,求矩形ABCD面積的最大值.
,求矩形ABCD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓C的中心在坐標原點,焦點在x軸上,橢圓C上的點到焦點距離的最大值為3,最小值為1.(1)求橢圓C的標準方程;(2)若直線l: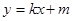 與橢圓C相交于A,B兩點(A,B不是左右頂點),且以AB為直徑的圓過橢圓C的右頂點。求證: 直線l過定點,并求出該定點的坐標.
與橢圓C相交于A,B兩點(A,B不是左右頂點),且以AB為直徑的圓過橢圓C的右頂點。求證: 直線l過定點,并求出該定點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com