對于每個實數x,設f(x)取y=2x-1,y=-2x+3兩個函數中的最小值,則f(x)的最大值是 .
【答案】
分析:在同一坐標系中分別做出函數y=2x-1,y=-2x+3兩個函數圖象,結合f(x)取y=2x-1,y=-2x+3兩個函數中的最小值,得到函數f(x)的圖象,數形結合易得答案.
解答:解:∵f(x)取y=2x-1,y=-2x+3兩個函數中的最小值,
故函數f(x)的圖象如圖中紅色線條所示:
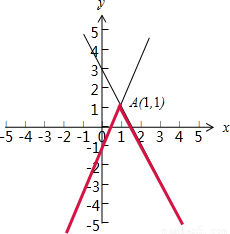
由圖易得f(x)的最大值是1
故答案為:1
點評:本題考查的知識點是分段函數及其圖象的作法,函數的最值,其中畫出函數圖象是解答的關鍵.
