
已知向量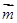 =(
=( sin
sin ,1),
,1),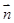 =(cos
=(cos ,cos2
,cos2 )
)
(1)若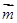 ·
·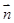 =1,求cos(
=1,求cos(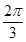 -x)的值;
-x)的值;
(2)記f(x)=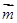 ·
·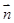 ,在△ABC中,角A,B,C的對邊分別是a,b,c,且滿足(2a-c)cosB=bcosC,求函數f(A)的取值范圍.
,在△ABC中,角A,B,C的對邊分別是a,b,c,且滿足(2a-c)cosB=bcosC,求函數f(A)的取值范圍.
(1)- .(2) (1,
.(2) (1,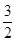 ).
).
解析試題分析:(1)∵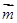 ·
·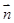 =1,即
=1,即 sin
sin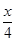 cos
cos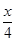 +cos2
+cos2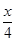 =1,
=1,
即 sin
sin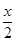 +
+ cos
cos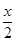 +
+ =1,
=1,
∴sin(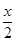 +
+ )=
)= .
.
∴cos(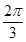 -x)=cos(x-
-x)=cos(x-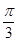 )=-cos(x+
)=-cos(x+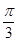 )=-[1-2sin2(
)=-[1-2sin2(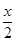 +
+ )]
)]
=2·( )2-1=-
)2-1=- .
.
(2)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC.
∴2sinAcosB-cosBsinC=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,∴sin(B+C)=sinA,且sinA≠0,
∴cosB= ,B=
,B=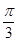 ,∴0<A<
,∴0<A<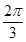 .
.
∴ <
<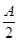 +
+ <
<
 <sin(
<sin(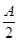 +
+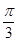 )<1.
)<1.
又∵f(x)=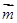 ·
·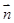 =sin(
=sin(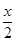 +
+ )+
)+ ,
,
∴f(A)=sin(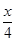 +
+ )+
)+ .
.
故函數f(A)的取值范圍是(1,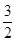 ).
).
考點:本題綜合考查了向量、三角函數及正余弦定理
點評:三角與向量是近幾年高考的熱門題型,這類題往往是先進行向量運算,再進行三角變換


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案科目:高中數學 來源: 題型:解答題
A、B是單位圓O上的動點,且A、B分別在第一、二象限.C是圓O與x軸正半軸的交點,△AOB為正三角形.記∠AOC=α.
(1)若A點的坐標為 ,求
,求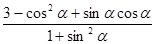 的值;
的值;
(2)求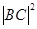 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
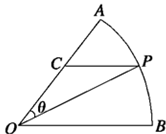
如圖所示,扇形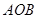 ,圓心角
,圓心角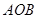 的大小等于
的大小等于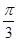 ,半徑為
,半徑為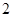 ,在半徑
,在半徑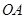 上有一動點
上有一動點 ,過點
,過點 作平行于
作平行于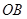 的直線交弧
的直線交弧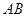 于點
于點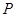 .
.
(1)若 是半徑
是半徑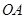 的中點,求線段
的中點,求線段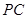 的大小;
的大小;
(2)設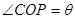 ,求△
,求△ 面積的最大值及此時
面積的最大值及此時 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com