
 ,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.
,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由. ,e])都有公共點,轉化為利用導數求函數y=f(x)在區間[
,e])都有公共點,轉化為利用導數求函數y=f(x)在區間[ ,e]上的值域.
,e]上的值域. ,e),f(x),f′(x)變化情況如下表:
,e),f(x),f′(x)變化情況如下表: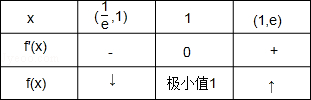
 )=2﹣
)=2﹣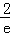 <2,
<2, ,e]上的值域為[1,2],
,e]上的值域為[1,2],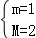 ,則對每一個t∈[m,M],直線y=t與曲線y=f(x)(x∈[
,則對每一個t∈[m,M],直線y=t與曲線y=f(x)(x∈[ ,e])都有公共點;
,e])都有公共點; ,e])都沒有公共點;
,e])都沒有公共點; ,e])都有公共點.
,e])都有公共點.

 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源:不詳 題型:解答題
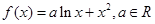
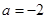 ,求證:函數
,求證:函數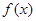 在(1,+∞)上是增函數;
在(1,+∞)上是增函數;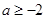 時,求函數
時,求函數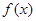 在[1,e]上的最小值及相應的x值;
在[1,e]上的最小值及相應的x值;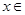 [l,e],使得
[l,e],使得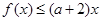 成立,求實數
成立,求實數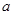 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
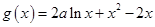 .
.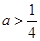 時,討論函數
時,討論函數 的單調性;
的單調性;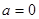 時,在函數
時,在函數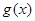 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為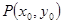 ,試探究函數
,試探究函數 在Q
在Q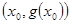 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?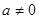 時
時 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
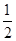 x2+2xf′(2014)+2014lnx,則f′(2014)=( )
x2+2xf′(2014)+2014lnx,則f′(2014)=( )| A.2015 | B.-2015 | C.2014 | D.-2014 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com