
�ژO����(bi��o)ϵ �У���֪����
�У���֪����
 �O(sh��)
�O(sh��) �c
�c �����c(di��n)
�����c(di��n)
��I�����c(di��n) �ĘO����(bi��o)��
�ĘO����(bi��o)��
��II�����(d��ng)ֱ�� �^�c(di��n)
�^�c(di��n) �����c����
�����c����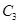 ���ڃɂ�(g��)��ͬ���c(di��n)
���ڃɂ�(g��)��ͬ���c(di��n) ��
��
 ����Сֵ.
����Сֵ.

| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ��,������(bi��o)ԭ�c(di��n)��O�c(di��n), �S�ķ�ؓ(f��)���S��O�S��������(bi��o)ϵ.��֪�c(di��n)
�S�ķ�ؓ(f��)���S��O�S��������(bi��o)ϵ.��֪�c(di��n)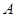 �ĘO����(bi��o)��
�ĘO����(bi��o)��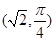 ,ֱ���ĘO����(bi��o)���̞�
,ֱ���ĘO����(bi��o)���̞� ,���c(di��n)
,���c(di��n)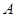 ��ֱ����.
��ֱ����.
(1)�� ��ֵ��ֱ����ֱ������(bi��o)����;
��ֵ��ֱ����ֱ������(bi��o)����;
(2)�Ac�ą���(sh��)���̞� ,(
,(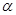 �酢��(sh��)),ԇ�Д�ֱ���c�A��λ���P(gu��n)ϵ.
�酢��(sh��)),ԇ�Д�ֱ���c�A��λ���P(gu��n)ϵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ �У�������
�������� �c
�c �Ľ��c(di��n)
�Ľ��c(di��n) �ĘO����(bi��o)��
�ĘO����(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ�У� ��O�c(di��n)���돽��2�ĈA
��O�c(di��n)���돽��2�ĈA �ĈA�ĵĘO����(bi��o)��
�ĈA�ĵĘO����(bi��o)�� .
.
��1����A �O����(bi��o)���̣�
�O����(bi��o)���̣�
��2�����ԘO�c(di��n)��ԭ�c(di��n)���ԘO�S�� �S�����S������ֱ������(bi��o)ϵ�У�ֱ��
�S�����S������ֱ������(bi��o)ϵ�У�ֱ�� �ą���(sh��)����
�ą���(sh��)����
�� (
( �酢��(sh��))��ֱ��
�酢��(sh��))��ֱ�� �c�A
�c�A �ཻ��
�ཻ�� ��
�� ���c(di��n)����֪���c(di��n)
���c(di��n)����֪���c(di��n) ��
��
��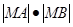 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(���}�M��10��)�x��4��4������(bi��o)ϵ�c����(sh��)����
��ֱ֪��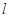 �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�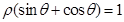 ������
������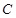 �ą���(sh��)���̞�
�ą���(sh��)���̞�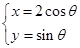 ��
��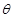 �酢��(sh��)����
�酢��(sh��)����
������ֱ��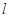 ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
�����O(sh��)ֱ��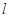 �c����
�c����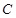 ����A��B���c(di��n)��ԭ�c(di��n)��
����A��B���c(di��n)��ԭ�c(di��n)��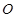 ����
����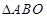 ����e��
����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
ƽ��ֱ������(bi��o)ϵ�У������� ��
�� �酢��(sh��)���ϵ�ÿһ�c(di��n)�v����(bi��o)��׃���M����(bi��o)׃?y��u)�ԭ����һ�룬Ȼ������(g��)�D������ƽ��
�酢��(sh��)���ϵ�ÿһ�c(di��n)�v����(bi��o)��׃���M����(bi��o)׃?y��u)�ԭ����һ�룬Ȼ������(g��)�D������ƽ�� ��(g��)��λ�����M����(bi��o)��׃���v����(bi��o)׃?y��u)�ԭ���?���õ�����
��(g��)��λ�����M����(bi��o)��׃���v����(bi��o)׃?y��u)�ԭ���?���õ����� ��������(bi��o)ԭ�c(di��n)��O�c(di��n)��
��������(bi��o)ԭ�c(di��n)��O�c(di��n)�� �ķ�ؓ(f��)���S��O�S�������ĘO����(bi��o)�е�����
�ķ�ؓ(f��)���S��O�S�������ĘO����(bi��o)�е����� �ķ��̞�
�ķ��̞� ����
���� ��
�� �����ҵ��L�ȣ�
�����ҵ��L�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�ژO����(bi��o)ϵ�У��O�c(di��n)������(bi��o)ԭ�c(di��n)O����֪�AC�ĈA������(bi��o)�� ���돽
���돽
�� ��ֱ��
��ֱ�� �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞� .
.
��1����AC�ĘO����(bi��o)���̣�
��2����AC��ֱ�� �ཻ��A��B���c(di��n)����AB���L.
�ཻ��A��B���c(di��n)����AB���L.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��С�}�M��14�֣�
��֪���� �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�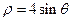 ���ԘO�c(di��n)��ԭ�c(di��n)���O�S��
���ԘO�c(di��n)��ԭ�c(di��n)���O�S��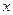 �S�ķ�ؓ(f��)���S����ƽ��ֱ������(bi��o)ϵ��ֱ��
�S�ķ�ؓ(f��)���S����ƽ��ֱ������(bi��o)ϵ��ֱ��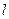 �ą���(sh��)���̞�
�ą���(sh��)���̞�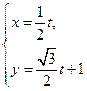 ��
��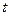 �酢��(sh��)������ֱ��
�酢��(sh��)������ֱ��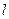 ������
������ �صõľ��ε��L��
�صõľ��ε��L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ����x�}
��D��ʾ��AB���Oֱ����CD�С�O��D��AB���L����CD���c(di��n)C������CAD��25�㣬�t��C��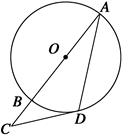
| A��45�� | B��40�� |
| C��35�� | D��30�� |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com