
已知數列 的前
的前 項和為
項和為 ,若
,若 ,
,
⑴證明數列 為等差數列,并求其通項公式;
為等差數列,并求其通項公式;
⑵令 ,①當
,①當 為何正整數值時,
為何正整數值時, :②若對一切正整數
:②若對一切正整數 ,總有
,總有 ,求
,求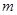 的取值范圍.
的取值范圍.
(1)證明詳見解析, ;(2)①
;(2)①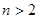 ,②
,②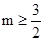 .
.
解析試題分析:(1)關于 和
和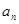 的遞推式,一般有兩種方法可解決,1:轉化為項的遞推式,根據遞推式 直接求通項公式,2:轉化為
的遞推式,一般有兩種方法可解決,1:轉化為項的遞推式,根據遞推式 直接求通項公式,2:轉化為 的遞推關系,先求
的遞推關系,先求 ,再求通項公式,該題已知數列前n項和
,再求通項公式,該題已知數列前n項和 和
和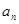 的遞推關系,由
的遞推關系,由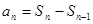 可的
可的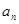 與
與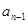 的關系,然后由等差數列定義證明,知道等差數列后再求通項公式;
的關系,然后由等差數列定義證明,知道等差數列后再求通項公式;
(2)①將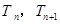 代入不等式,解不等式可得,②恒成立問題往往可以采取參變分離的方法,
代入不等式,解不等式可得,②恒成立問題往往可以采取參變分離的方法,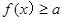 或
或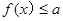 的形式,最后轉化為求函數
的形式,最后轉化為求函數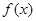 最值,即
最值,即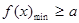 或
或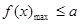 ,該題可轉化為求
,該題可轉化為求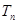 的最大值問題,求
的最大值問題,求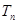 的最大值可以結合函數的函數或者單調性處理,但是注意定義域
的最大值可以結合函數的函數或者單調性處理,但是注意定義域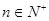 .
.
試題解析:(1)令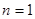 ,
,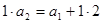 ,即
,即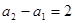 ,由
,由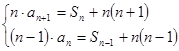
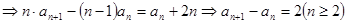
∵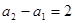 ,∴
,∴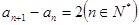 ,
,
即數列 是以2為首項,2為公差的等差數列, ∴
是以2為首項,2為公差的等差數列, ∴
(2)①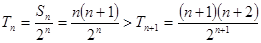 ,即
,即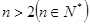 ②∵
②∵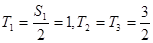 ,又∵
,又∵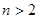 時,
時,
∴各項中數值最大為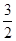 ,∵對一切正整數
,∵對一切正整數 ,總有
,總有 恒成立,因此
恒成立,因此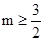 .
.
考點:1、等差數列的定義和通項公式;2、恒成立問題.


科目:高中數學 來源: 題型:解答題
觀察下列三角形數表,假設第n行的第二個數為an(n≥2,n∈N*).
(1)依次寫出第六行的所有6個數;
(2)歸納出an+1與an的關系式并求出{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知{an}是等差數列,a1=3,Sn是其前n項和,在各項均為正數的等比數列{bn}中,b1=1,且b2+S2=10,S5 =5b3+3a2.
(I )求數列{an}, {bn}的通項公式;
(II)設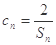 ,數列{cn}的前n項和為Tn,求證
,數列{cn}的前n項和為Tn,求證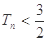
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列 是等差數列,且
是等差數列,且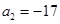 ,
,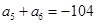 ;又若
;又若 是各項為正數的等比數列,且滿足
是各項為正數的等比數列,且滿足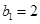 ,其前
,其前 項和為
項和為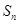 ,
,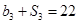 .
.
(1)分別求數列 ,
, 的通項公式
的通項公式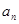 ,
,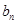 ;
;
(2)設數列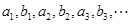 的前
的前 項和為
項和為 ,求
,求 的表達式,并求
的表達式,并求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于任意的 (
( 不超過數列的項數),若數列的前
不超過數列的項數),若數列的前 項和等于該數列的前
項和等于該數列的前 項之積,則稱該數列為
項之積,則稱該數列為 型數列。
型數列。
(1)若數列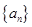 是首項
是首項 的
的 型數列,求
型數列,求 的值;
的值;
(2)證明:任何項數不小于3的遞增的正整數列都不是 型數列;
型數列;
(3)若數列 是
是 型數列,且
型數列,且 試求
試求 與
與 的遞推關系,并證明
的遞推關系,并證明 對
對 恒成立。
恒成立。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列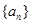 的各項均為正數,
的各項均為正數,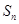 為其前
為其前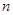 項和,對于任意的
項和,對于任意的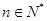 ,滿足關系式
,滿足關系式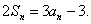
(1)求數列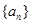 的通項公式;
的通項公式;
(2)設數列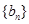 的通項公式是
的通項公式是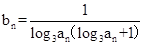 ,前
,前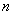 項和為
項和為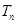 ,求證:對于任意的正整數
,求證:對于任意的正整數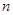 ,總有
,總有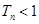 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com