
 .
. ,利用等差數列的通項公式列出方程組,求出公差,由此能求出{an}的通項公式.
,利用等差數列的通項公式列出方程組,求出公差,由此能求出{an}的通項公式. =-2cos2πx+2,其最小正周期為
=-2cos2πx+2,其最小正周期為 =1,故首項為1,由公比q=3,知
=1,故首項為1,由公比q=3,知 ,由此能求出數列{an-bn}的前n項和Sn.
,由此能求出數列{an-bn}的前n項和Sn.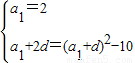 ,
, =-2cos2πx+2,
=-2cos2πx+2, =1,
=1, ,
,

 -
- •3n.
•3n.

 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 21 |
| 8 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 2 |
| 2n+a1 |
| 2 |
| 2n+a2 |
| 2 |
| 2n+an |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com