
題目列表(包括答案和解析)
(17)(本小題滿分10分)
已知隨機變量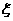 的分布列為
的分布列為
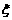 |
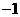 |
0 |
1 |
2 |
3 |
|
P |
0.3 |
0.1 |
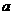 |
0.3 |
0.2 |
求實數a的值,并求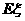 和
和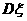 .
.
(18)(本小題滿分12分)
已知函數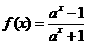
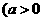 ,
,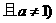 .
.
(Ⅰ)求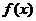 的反函數
的反函數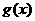 ;
;
(Ⅱ)若函數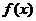 過點
過點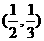 ,則函數
,則函數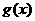 過點
過點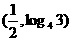 嗎?為什么?
嗎?為什么?
(19)(本小題滿分12分)
已知正三棱柱ABC-A1B1C1,底面邊長AB=2,AB1⊥BC1,點O、O1分別是
 邊AC、A1C1的中點,建立如圖所示的空間直角坐標系.
邊AC、A1C1的中點,建立如圖所示的空間直角坐標系.
(Ⅰ)求正三棱柱ABC-A1B1C1的側棱長;
(Ⅱ)求異面直線AB1與BC所成角的大小.
(20)(本小題滿分12分)
如圖,有甲乙兩個村莊,甲村位于一直線河岸的岸邊A處,乙村與甲村在河的同側,乙村位于離河岸40km的B處,乙村到河岸的垂足D與A相距50km,兩村要在此岸邊合建一個自來水廠C,從自來水廠到甲村和乙村的水管費用分別為每千米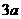 元和
元和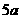 元. 現要進行工程費用測算.
元. 現要進行工程費用測算.
(Ⅰ)求出水管總費用關于水廠C到D的距離的函數
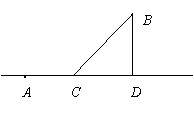 關系式;
關系式;
(Ⅱ)問自來水廠C建在何處,才能使水管總費用最
省?
(21)(本小題滿分14分)
在以O為原點的直角坐標系中,點A(3,-1)為 的直角頂點. 已知|AB|=2|OA|,且點B的縱坐標大于零.
的直角頂點. 已知|AB|=2|OA|,且點B的縱坐標大于零.
(Ⅰ)求向量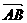 的坐標;
的坐標;
(Ⅱ)是否存在實數a,使二次函數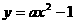 的圖像上總有關于直線OB對稱的兩個不同的點?若不存在,說明理由;若存在,求a的取值范圍.
的圖像上總有關于直線OB對稱的兩個不同的點?若不存在,說明理由;若存在,求a的取值范圍.
(22)(本小題滿分14分)
若數列{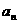 }的通項
}的通項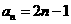 ,設數列{
,設數列{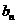 }的通項
}的通項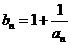 ,又記
,又記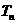 是數列{
是數列{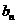 }
}
的前n項的積.
(Ⅰ)求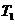 ,
,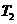 ,
,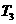 的值;
的值;
(Ⅱ)試比較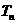 與
與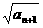 的大小,并證明你的結論.
的大小,并證明你的結論.
(13)若復數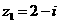 ,
,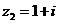 ,則
,則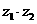 的模為__________.
的模為__________.
(14)若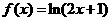 ,則
,則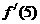 =
.
=
.
(15)已知函數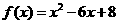
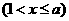 ,并且函數
,并且函數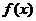 的最小值為
的最小值為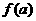 ,則實數
,則實數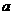 的取值范圍是
.
的取值范圍是
.
(16)在某次花樣滑冰比賽中,發生裁判受賄事件,競賽委員會決定將裁判由原來的9名增至14名,但只任取其中7名裁判的評分作為有效分. 若14名裁判中有2人受賄,則有效分中沒有受賄裁判的評分的概率是 (結果用數值表示).
一項是符合題目要求的.
(1)集合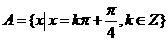 ,
,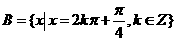 ,則有
,則有
(A)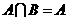 (B)
(B)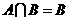 (C)
(C)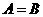 (D)
(D)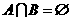
(2)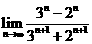 等于
等于
(A)0
(B)1 (C)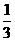 (D)
(D)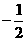
(3)某單位有職工160人,其中業務人員120人,管理人員16人,后勤人員24人. 為了
了解職工的某種情況,要從中抽取一個容量為20的樣本. 若要用分層抽樣的方法,則抽
取的業務人員,管理人員,后勤人員的人數分別為
(A)7、6、7 (B)15、2、3 (C)10、4、6 (D)17、1、2
(4)已知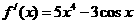 ,
, ,則
,則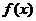 等于
等于
(A)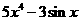 (B)
(B)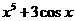 (C)
(C)
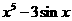 (D)
(D) 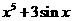
(5)復數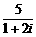 的共軛復數是
的共軛復數是
(A)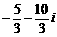 (B)
(B)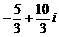 (C)
(C)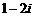 (D)
(D)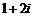
(6)已知命題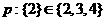 ,命題
,命題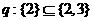 ,有如下判斷:①
,有如下判斷:①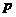 或
或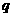 為真;②
為真;② 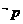 或
或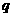 為假;③
為假;③ 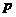 且
且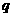 為真;④
為真;④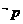 為真.其中正確的是
為真.其中正確的是
(A)①② (B)①④ (C)②④ (D)③④
(7)給定兩個向量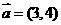 ,
,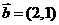 ,
,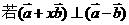 ,則x的值等于
,則x的值等于
(A)-3
(B)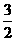 (C)3 (D)-
(C)3 (D)-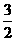
(8)已知函數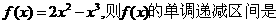
(A)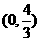 (B)
(B)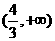 (C)
(C)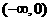 (D)
(D)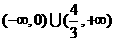
(9)設函數f ( x ) 是定義域為R且周期為3的奇函數,若 f ( 1 ) =1 ,f ( 2 ) = a ,則
(A) a =1 (B) a = -1 (C) a = 2 (D) a= -2
(10)從甲地到乙地通話m分鐘的電話費由函數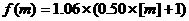 給出,其中m>0, [m]表示大于或等于m的最小整數,如:[3]=3,[3.1]=4, [3.7]=4,則從甲地到乙地通話時間為5.5分鐘的電話費為
給出,其中m>0, [m]表示大于或等于m的最小整數,如:[3]=3,[3.1]=4, [3.7]=4,則從甲地到乙地通話時間為5.5分鐘的電話費為
(A)3.71元 (B)3.97元 (C) 4.71元 (D) 4.24元
(11)設A、B、C、D是空間不共面的四點,且滿足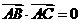 ,
,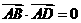 ,
,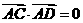 則△BCD是
則△BCD是
(A) 銳角三角形 (B) 直角三角形
(C) 鈍角三角形 (D) 以上都有可能
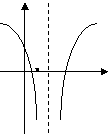
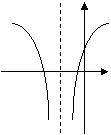 (12)函數
(12)函數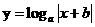 (
(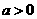 ,
,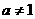 ,
,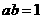 )的圖象可能是
)的圖象可能是
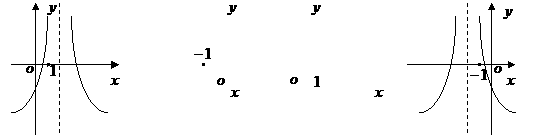 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
第Ⅱ卷(非選擇題 共90分)
第Ⅱ卷全部是非選擇題,必須在答題區域內,用黑色字跡的鋼筆或簽字筆作答,不能答在試卷上,否則答案無效.
22.(本小題滿分14分)
對于函數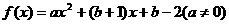 ,若存在實數
,若存在實數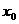 ,使
,使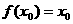 成立,則稱
成立,則稱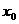 為
為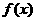 的不動點.
的不動點.
(1)當a=2,b=-2時,求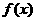 的不動點;
的不動點;
(2)若對于任何實數b,函數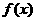 恒有兩相異的不動點,求實數a的取值范圍;
恒有兩相異的不動點,求實數a的取值范圍;
(3)在(2)的條件下,若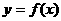 的圖象上A、B兩點的橫坐標是函數
的圖象上A、B兩點的橫坐標是函數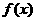 的不動點,
的不動點,
且直線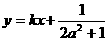 是線段AB的垂直平分線,求實數b的取值范圍.
是線段AB的垂直平分線,求實數b的取值范圍.
[機密★啟用前]
21.(本小題滿分12分)
已知點H(-6,0),點P在y軸上,點Q在x軸的正半軸上,點M在直線PQ上,且滿足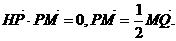
(1)當點P在y軸上移動時,求點M的軌跡C;
(2)過點T(-2,0)作直線l與軌跡C交于A、B兩點,若在x軸上存在一點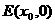 ,
,
使得△AEB是以點E為直角頂點的直角三角形,求直線l的斜率k的取值范圍.
20.(本小題滿分12分)
設數列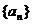 是等比數列,
是等比數列,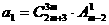 ,公比q是
,公比q是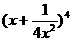 的展開式中的第二項
的展開式中的第二項
(按x的降冪排列).
(1)用n,x表示通項an與前n項和Sn;
(2)若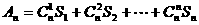 ,用n,x表示An.
,用n,x表示An.
19.(本小題滿分12分)
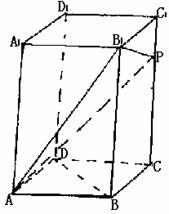
在正四棱柱ABCD-A1B1C1D1中,側棱是底面邊長的2倍,P是側棱CC1上的任一點.
(1)求證:不論P在側棱CC1上何位置,總有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P與平面ABCD所成二面角的余弦值;
(3)當P點在側棱CC1上何處時,AP在平面B1AC上的射影是∠B1AC的平分線.
18.(本小題滿分12分)
為了測試甲、乙兩名射擊運動員的射擊水平,讓他們各向目標靶射出10次,其中甲擊中目標7次,乙擊中目標6次,若再讓甲、乙兩人各自向目標靶射擊3次,求:
(1)甲運動員恰好擊中目標2次的概率是多少?
(2)兩名運動員都恰好擊中目標2次的概率是多少?(結果保留兩個有效數字).
17.(本小題滿分12分)
△ABC中,三個內角分別是A、B、C,向量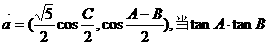
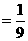 時,求
時,求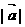 .
.
16.過雙曲線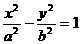 的右焦點F(c,0)的直線交雙曲線于M、N兩點,交y軸于P
的右焦點F(c,0)的直線交雙曲線于M、N兩點,交y軸于P
點,則有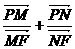 的定值為
的定值為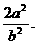 類比雙曲線這一結論,在橢圓
類比雙曲線這一結論,在橢圓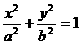 (a>b
(a>b
>0)中,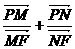 是定值
.
是定值
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com